Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
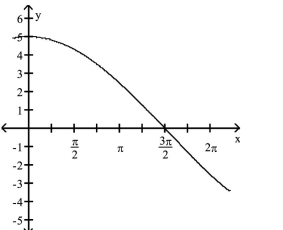
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (46)
(46)
Use a table or a calculator to evaluate the function. Round to four decimal places.
-sec
(Multiple Choice)
4.8/5  (39)
(39)
Use a table or a calculator to evaluate the function. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (27)
(27)
Match the function with its graph.
-1)
2)
3)
4)
A.
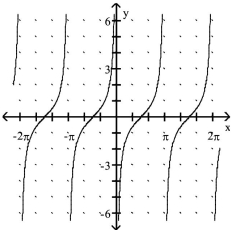 B.
B.
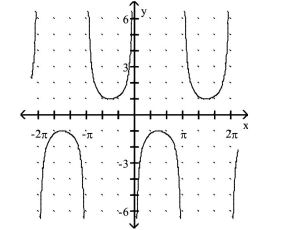 C.
C.
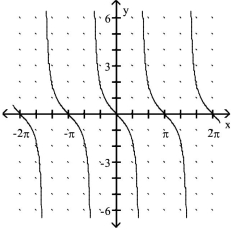 D.
D.
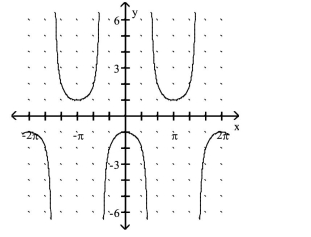
(Multiple Choice)
4.8/5  (31)
(31)
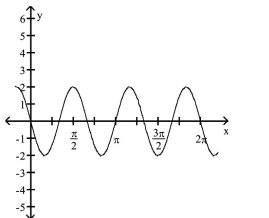
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (33)
(33)
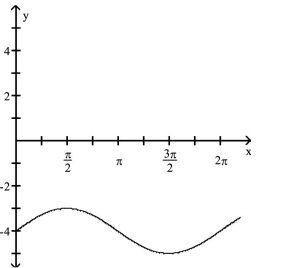
The function graphed is of the form y = cos x + c, y = sin x + c, y = cos(x - d), or y = sin(x - d), where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (39)
(39)
Use the formula to find the value of the missing variable. Give an exact answer unless otherwise indicated.
- radian per
(Multiple Choice)
5.0/5  (33)
(33)
Solve the problem.
-A weight attached to a spring is pulled down 5 inches below the equilibrium position. Assuming that the period of the system is second, determine a trigonometric model that gives the position of the weight at time seconds.
(Multiple Choice)
4.8/5  (32)
(32)
Use the formula to find the value of the missing variable. Give an exact answer.
- radian per
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-The position of a weight attached to a spring is inches after seconds. When does the weight first reach its maximum height?
(Multiple Choice)
4.8/5  (33)
(33)
Find the value of s in the interval [0, π/2] that makes the statement true. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-The path of a projectile fired at an inclination to the horizontal with an initial speed is a parabola. The range of the projectile, the horizontal distance that the projectile travels, is found by the formula where feet per second per second or meters per second per second. Find the range of a projectile fired with an initial velocity of 144 feet per second at an angle of to the horizontal. Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (28)
(28)
Solve the problem.
-Two wheels are rotating in such a way that the rotation of the smaller wheel causes the larger wheel to rotate. The radius of the smaller wheel is centimeters and the radius of the larger wheel is centimeters. Through how many degrees (to the nearest hundredth of a degree) will the larger wheel rotate if the smaller one rotates ?
(Multiple Choice)
4.9/5  (27)
(27)
Showing 141 - 160 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)