Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Use a table or a calculator to evaluate the function. Round to four decimal places.
-
(Multiple Choice)
5.0/5  (38)
(38)
Solve the problem.
-Find the radius (to the nearest hundredth of a millimeter) of a pulley if rotating the pulley raises the pulley .
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-Let angle POQ be designated . Angles and VRQ are right angles. If , find the length of PQ accurate to four decimal places.
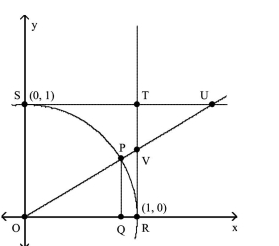
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Suppose that the average monthly low temperatures for a small town are shown in the table.
\begin{tabular} { l | l l l l l l l l l l l l }
Month & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\
\hline Temperature & 19 & 27 & 38 & 45 & 57 & 62 & 65 & 58 & 51 & 41 & 33 & 25
\end{tabular}
Model this data using .
(Multiple Choice)
4.9/5  (38)
(38)
Find the length of an arc intercepted by a central angle θin a circle of radius r. Round your answer to 1 decimal place.
- .; radians
(Multiple Choice)
4.8/5  (34)
(34)
Find the exact value of s in the given interval that has the given circular function value.
-
(Multiple Choice)
4.9/5  (36)
(36)
Assume that the cities lie on the same north-south line and that the radius of the earth is 6400 km.
-Find the latitude of Spokane, WA if Spokane and Jordan Valley, OR, , are apart.
(Multiple Choice)
4.9/5  (33)
(33)
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .
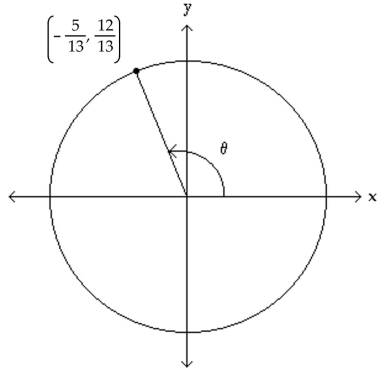
(Multiple Choice)
4.8/5  (42)
(42)
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-Find the radius of a circle in which a central angle of radian determines a sector of area 56 square meters. Round to the nearest hundredth.
(Multiple Choice)
4.8/5  (36)
(36)
Use a table or a calculator to evaluate the function. Round to four decimal places.
-
(Multiple Choice)
5.0/5  (33)
(33)
Find the area of a sector of a circle having radius r and central angle θ. If necessary, express the answer to the nearest
tenth.
- radians
(Multiple Choice)
4.9/5  (37)
(37)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-A rotating beacon is located 3 ft from a wall. The distance from the beacon to the point on the wall where the beacon is aimed is given by
where is time measured in seconds since the beacon started rotating. Find for seconds. Round your answer to the nearest hundredth.
(Multiple Choice)
4.7/5  (36)
(36)
Use the formula to find the value of the missing variable. Give an exact answer.
-
(Multiple Choice)
4.9/5  (36)
(36)
Showing 261 - 280 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)