Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
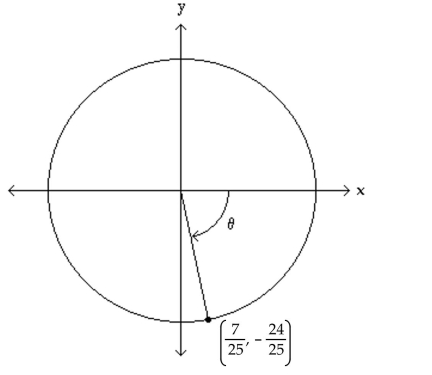
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .
(Multiple Choice)
4.9/5  (41)
(41)
Use a table or a calculator to evaluate the function. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-An object is spinning around a circle with a radius of 19 centimeters. If in 9 seconds a central angle of radian has been covered, what is the linear speed of the object?
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-Ignoring friction, the time, (in seconds), required for a block to slide down an inclined plane is given by the formula where is the length of the base in feet and feet per second is the acceleration of gravity. How long does it take a block to slide down an inclined plane with a base of 12 feet at an angle of ? Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The minimum length of a highway sag curve can be computed by
where is the downhill grade in degrees is the uphill grade in degrees is the safe stopping distance for a given speed limit, is the height of the headlights, and is the alignment of the headlights in degrees. Compute for a 55 -mph speed limit, where , , and . Round your answer to the nearest foot.
(Multiple Choice)
4.9/5  (35)
(35)
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π.
-
(Multiple Choice)
4.8/5  (43)
(43)
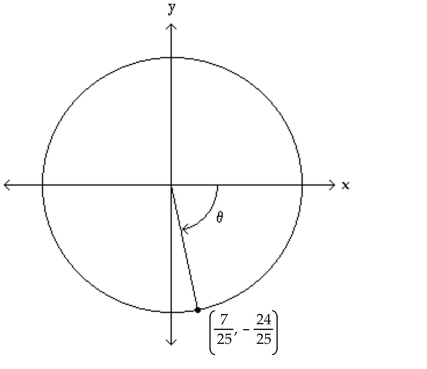
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find
(Multiple Choice)
4.9/5  (37)
(37)
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π.
-
(Multiple Choice)
4.9/5  (33)
(33)
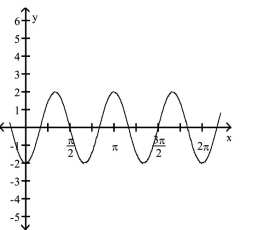
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (36)
(36)
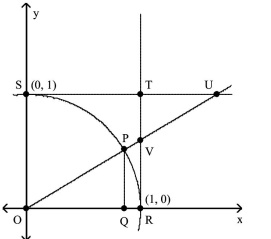
Solve the problem.
-Let angle be designated . Angles and are right angles. If , find the exact length of US.
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The minute hand of a clock is 14 inches long. What distance does its tip move in 23 minutes? Give an exact answer.
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The voltage in an electrical circuit is given by , where is time measured in seconds. Find the amplitude.
(Multiple Choice)
4.8/5  (26)
(26)
Solve the problem.
-A spring with a spring constant of 6 and a 1-unit mass attached to it is stretched and released. What is the equation for the resulting oscillatory motion?
(Multiple Choice)
4.7/5  (27)
(27)
Find the value of s in the interval [0, π/2] that makes the statement true. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
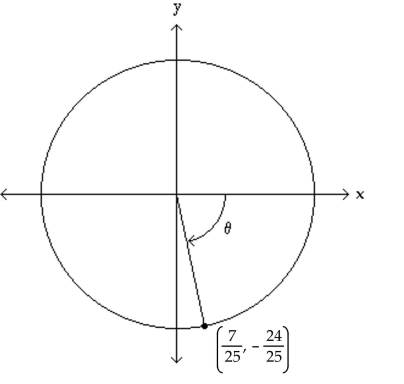
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-A sensor light installed on the edge of a home can detect motion for a distance of . in front and with a range of motion of . Over what area will the sensor detect motion and become illuminated? Round to the nearest hundredth.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 241 - 260 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)