Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Assume that the cities lie on the same north-south line and that the radius of the earth is 6400 km.
-Find the latitude of Winnipeg, Canada if Winnipeg and Austin, TX, , are apart.
(Multiple Choice)
4.9/5  (34)
(34)
Convert the radian measure to degrees. Give answer using decimal degrees to the nearest hundredth. Use 3.1416 for π.
-
(Multiple Choice)
4.8/5  (40)
(40)
Match the function with its graph.
-1)
2)
3)
4)
A.
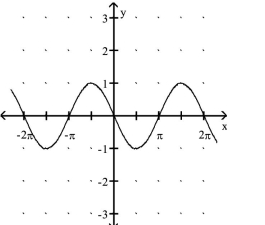 B.
B.
 C.
C.
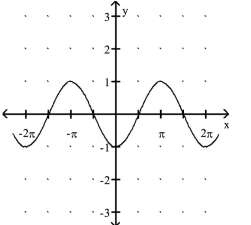 D.
D.
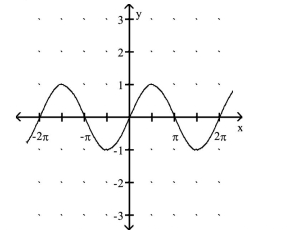
(Multiple Choice)
4.9/5  (43)
(43)
Find the exact values of s in the given interval that satisfy the given condition.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Two pulleys of diameters and are connected by a belt. The larger pulley rotates 44 times per min. Find the angular speed of the smaller pulley.
(Multiple Choice)
4.9/5  (37)
(37)
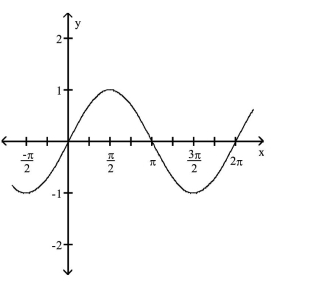
The function graphed is of the form y = cos x + c, y = sin x + c, y = cos(x - d), or y = sin(x - d), where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-Write the equation that describes the simple harmonic motion of a particle moving uniformly around a circle of radius 7 units, with angular speed 2 radians per second.
(Multiple Choice)
4.8/5  (30)
(30)
Graph the function over a one-period interval.
- y=-4(x-\pi)
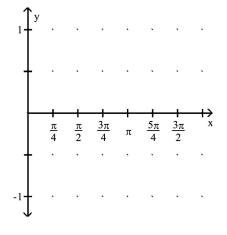
(Multiple Choice)
4.7/5  (31)
(31)
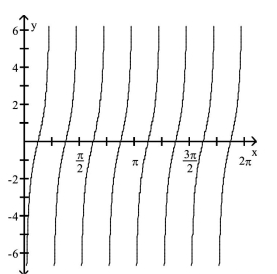
The function graphed is of the form y = a tan bx or y = a cot bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (34)
(34)
Match the function with its graph.
-1)
2)
3)
4)
A.
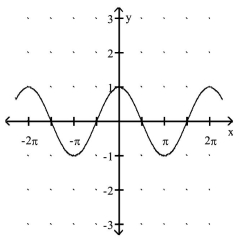 B.
B.
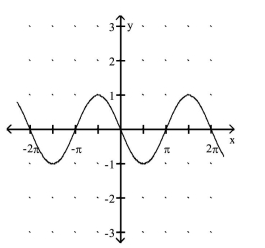 C.
C.
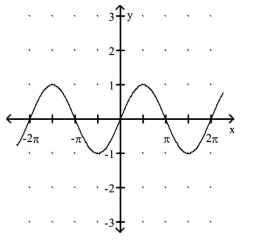 D.
D.
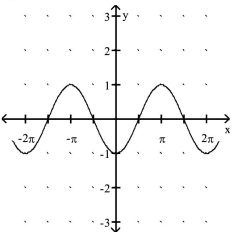
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A pendulum of length , when displaced horizontally and released, oscillates with harmonic motion according to the equation , where is the distance in meters from the rest position seconds after release, and . Identify the period, amplitude, and phase shift when and . Round all answers to the nearest hundredth.
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-A pulley rotates through in one minute. How many rotations (to the nearest tenth of a rotation) does the pulley make in an hour?
(Multiple Choice)
4.8/5  (31)
(31)
Find the area of a sector of a circle having radius r and central angle θ. If necessary, express the answer to the nearest
tenth.
- radians
(Multiple Choice)
4.8/5  (41)
(41)
Find the area of a sector of a circle having radius r and central angle θ. If necessary, express the answer to the nearest
tenth.
-
(Multiple Choice)
4.8/5  (29)
(29)
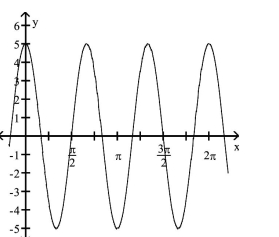
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-A weight attached to a spring is pulled down 9 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time seconds.
(Multiple Choice)
4.9/5  (39)
(39)
Showing 101 - 120 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)