Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Solve the problem.
-Suppose that a weight on a spring has an initial position of inches and a period of seconds. Find a function that models the displacement of the weight.
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-The chart represents the amount of fuel consumed by a machine used in manufacturing. The machine is turned on at the beginning of the day, takes a certain amount of time to reach its full power (the point at which it uses the most fuel per hour), runs for a certain number of hours, and is shut off at the end of the work day. The fuel usage per hour of the machine is represented by a periodic function. When does the machine first reach its full power?
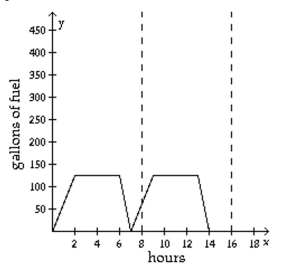
(Multiple Choice)
4.9/5  (29)
(29)
Solve the problem.
-A pendulum swinging through a central angle of completes an arc of length . What is the length of the pendulum? Round to the nearest hundredth.
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-A weight attached to a spring is pulled down 7 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time second.
(Multiple Choice)
4.8/5  (30)
(30)
Provide an appropriate response.
-Describe how an angle measure can be converted from radians to degrees.
(Multiple Choice)
4.8/5  (37)
(37)
Convert the degree measure to radians. Leave answer as a multiple of π.
-
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-Find the measure (in radians) of a central angle of a sector of area 45 square inches in a circle of radius 9 inches. Round to the nearest hundredth.
(Multiple Choice)
4.8/5  (35)
(35)
Match the function with its graph.
-1)
2)
3)
4)
A.
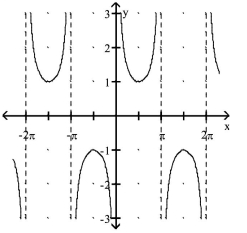 B.
B.
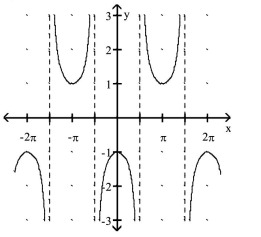 C.
C.
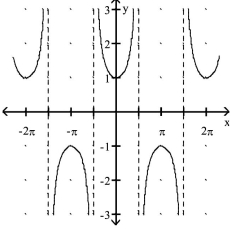 D.
D.
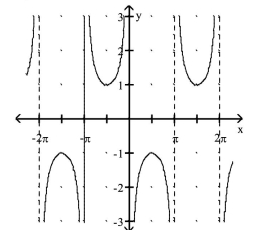
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-The position of a weight attached to a spring is inches after seconds. What is the maximum height that the weight reaches above the equilibrium position and when does it first reach the maximum height?
(Multiple Choice)
4.9/5  (38)
(38)
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π.
-
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-A weight attached to a spring is pulled down 4 inches below the equilibrium position. Assuming that the period of the system is , what is the frequency of the system?
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-Suppose the tip of the minute hand of a clock is 8 in. from the center of the clock. Determine the distance traveled by the tip of the minute hand in hours. Give an exact answer.
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The temperature in Fairbanks is approximated by
where is the temperature on day , with corresponding to Jan. 1 and corresponding to Dec. 31. Estimate the temperature on day 230 .
(Multiple Choice)
4.9/5  (26)
(26)
Solve the problem.
-A generator produces an alternating current according to the equation , where is time in seconds and is the current in amperes. What is the smallest time such that ?
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-The position of a weight attached to a spring is inches after seconds. What is the maximum height that the weight rises above the equilibrium position?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 201 - 220 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)