Exam 8: Inferences Based on a Single

A method currently used by doctors to screen women for possible breast cancer fails to detect cancer in 20% of women who actually have the disease. A new method has been developed that researchers hope will be able to detect cancer more accurately. A random sample of 80 women known to have breast cancer were screened using the new method. Of these, the new method failed to detect cancer in 9. Is the sample size sufficiently large to conduct this test of hypothesis? Explain.

(Essay)

4.8/5

(32)

Question 21

Consider the following printout. HYPOTHESIS: VARIANCE $\mathrm { X } = \mathrm { x }$ $X = \text { gpa }$ SAMPLE MEAN OF $X = 2.8731$ SAMPLE VARIANCE OF $X = .18000$ SAMPLE SIZE OF $X = 189$ HYPOTHESIZED VALUE $( x ) = 3.0$ VARIANCE $\mathrm { X } - \mathrm { x } = - .1269$ $z = - 4.11203$ State the proper conclusion when testing $H _ { 0 } : \mu = 3.0$ vs. $H _ { \mathrm { a } } : \mu < 3.0$ at $\alpha = .05$ .

(Multiple Choice)

4.8/5

(38)

Question 22

A __________ is a numerical quantity computed from the data of a sample and is used in reaching a decision on whether or not to reject the null hypothesis.

(Multiple Choice)

4.7/5

(34)

Question 23

A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they Spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the universityʹs students differed from 20 minutes. Suppose the large-sample test statistic was calculated to be z = 2.14. Find the p-value For this test of hypothesis.

(Multiple Choice)

4.7/5

(37)

Question 24

$\text { Let } \chi _ { 0 } ^ { 2 } \text { be a particular value of } \chi ^ { 2 } \text {. Find the value of } \chi _ { 0 } ^ { 2 } \text { such that } \mathrm { P } \left( \chi ^ { 2 } > \chi _ { 0 } ^ { 2 } \right) = .10 \text { for } n = 10 \text {. }$

(Multiple Choice)

5.0/5

(30)

Question 25

A test of hypothesis was performed to determine if the true proportion of college students who preferred a particular brand of soda differs from .50. The ASP printout is supplied below. Note: All Data refer to the proportion of students who preferred the brand of soda. HYPOTHESIS: PROPORTION $\mathrm { X } = \mathrm { x }$ $A test of hypothesis was performed to determine if the true proportion of college students who preferred a particular brand of soda differs from .50. The ASP printout is supplied below. Note: All Data refer to the proportion of students who preferred the brand of soda. HYPOTHESIS: PROPORTION \mathrm { X } = \mathrm { x } State the proper conclusion if the test was conducted at \alpha = .10 .$ State the proper conclusion if the test was conducted at $\alpha = .10$ .

(Multiple Choice)

4.8/5

(35)

Question 26

A random sample of 8 observations from an approximately normal distribution is shown below. 5 6 4 5 8 6 5 3 Find the observed level of significance for the test of $H _ { 0 } : \mu = 5$ against $H _ { \mathrm { a } } : \mu \neq 5$ . Interpret the result.

(Essay)

4.9/5

(39)

Question 27

An insurance company sets up a statistical test with a null hypothesis that the average time for processing a claim is 7 days, and an alternative hypothesis that the average time for processing a Claim is greater than 7 days. After completing the statistical test, it is concluded that the average Time exceeds 7 days. However, it is eventually learned that the mean process time is really 7 days. What type of error occurred in the statistical test?

(Multiple Choice)

4.8/5

(33)

Question 28

The value of $\beta$ is the area under the bell curve for the distribution of $\bar { x }$ centered at $\mu _ { \mathrm { a } }$ for values of $\bar { x }$ that fall within the acceptance region of the distribution of $\bar { x }$ centered at $\mu _ { 0 }$ .

(Multiple Choice)

4.9/5

(37)

Question 29

A small private college is interested in determining the percentage of its students who live off campus and drive to class. Specifically, it was desired to determine if less than 20% of their current Students live off campus and drive to class. The college decided to take a random sample of 108 of Their current students to use in the analysis. Is the sample size of n = 108 large enough to use this Inferential procedure?

(Multiple Choice)

4.9/5

(40)

Question 30

A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are Beginning to increase in price because of added features. According to the story, the average price Of all digital cameras a couple of years ago was $215.00. A random sample of cameras was recently Taken and entered into a spreadsheet. It was desired to test to determine if that average price of all Digital cameras is now more than $215.00. The information was entered into a spreadsheet and the Following printout was obtained: One-Sample T Test Null Hypothesis: $\mu = 215$ Alternative Hyp: $\mu > 215$ $A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are Beginning to increase in price because of added features. According to the story, the average price Of all digital cameras a couple of years ago was $215.00. A random sample of cameras was recently Taken and entered into a spreadsheet. It was desired to test to determine if that average price of all Digital cameras is now more than $215.00. The information was entered into a spreadsheet and the Following printout was obtained: One-Sample T Test Null Hypothesis: \mu = 215 Alternative Hyp: \mu > 215 Is a sample size \mathrm { n } = 22 large enough to utilize the central limit theorem in this inferential procedure?$ Is a sample size $\mathrm { n } = 22$ large enough to utilize the central limit theorem in this inferential procedure?

(Multiple Choice)

4.8/5

(33)

Question 31

A revenue department is under orders to reduce the time small business owners spend filling out pension form ABC-5500. Previously the average time spent on the form was 6.3 hours. In order to Test whether the time to fill out the form has been reduced, a sample of 48 small business owners Who annually complete the form was randomly chosen, and their completion times recorded. The Mean completion time for ABC-5500 form was 5.7 hours with a standard deviation of 1.8 hours. In Order to test that the time to complete the form has been reduced, state the appropriate null and Alternative hypotheses.

(Multiple Choice)

4.8/5

(33)

Question 32

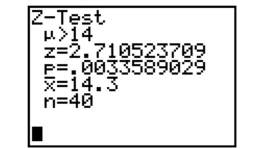
Based on the information in the screen below, what would you conclude in the test of $H_{0}: \mu \leq 14, H_{\mathrm{a}}: \mu>14 \text {. Use } \alpha=.01$ $Based on the information in the screen below, what would you conclude in the test of H_{0}: \mu \leq 14, H_{\mathrm{a}}: \mu>14 \text {. Use } \alpha=.01$

(Essay)

4.7/5

(38)

Question 33

Suppose we wish to test $H _ { 0 } : \mu = 39$ vs. $H _ { \mathrm { a } } : \mu < 39$ . Which of the following possible sample results gives the most evidence to support $H _ { \text {a } }$ (i.e., reject $H _ { 0 }$ )?

(Multiple Choice)

4.9/5

(33)

Question 34

The alternative hypothesis is accepted as true unless there is overwhelming evidence that it is false.

(True/False)

4.7/5

(42)

Question 35

Identify the observed level of significance for the test summarized on the screen below and interpret its value.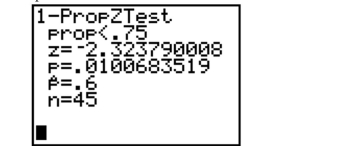

(Essay)

4.9/5

(38)

Question 36

It is desired to test $\mathrm { H } _ { 0 } : \mu = 50$ against $\mathrm { H } _ { \mathrm { A } } : \mu \neq 50$ using $\alpha = 0.10$ . The population in question is uniformly distributed with a standard deviation of 15. A random sample of 49 will be drawn from this population. If $\mu$ is really equal to 45 , what is the power of the test?

(Multiple Choice)

4.9/5

(38)

Question 37

A method currently used by doctors to screen women for possible breast cancer fails to detect cancer in 20% of women who actually have the disease. A new method has been developed that researchers hope will be able to detect cancer more accurately. A random sample of 90 women known to have breast cancer were screened using the new method. Of these, the new method failed to detect cancer in eight. Specify the null and alternative hypotheses that the researchers wish to test.

(Essay)

4.9/5

(42)

Question 38

A bottling company produces bottles that hold 8 ounces of liquid. Periodically, the company gets complaints that their bottles are not holding enough liquid. To test this claim, the bottling Company randomly samples 16 bottles and finds the average amount of liquid held by the bottles Is 7.7 ounces with a standard deviation of .4 ounce. Calculate the appropriate test statistic.

(Multiple Choice)

4.8/5

(33)

Question 39

How many tissues should a package of tissues contain? Researchers have determined that a person uses an average of 40 tissues during a cold. Suppose a random sample of 2500 people yielded the following data on the number of tissues used during a cold: $\bar { x } = 34 , s = 20$ . Suppose the corresponding test statistic falls in the rejection region at $\alpha = .05$ . What is the correct conclusion?

(Multiple Choice)

5.0/5

(36)

Question 40

Showing 21 - 40 of 144

A __________ is a numerical quantity computed from the data of a sample and is used in reaching a decision on whether or not to reject the null hypothesis.

$\text { Let } \chi _ { 0 } ^ { 2 } \text { be a particular value of } \chi ^ { 2 } \text {. Find the value of } \chi _ { 0 } ^ { 2 } \text { such that } \mathrm { P } \left( \chi ^ { 2 } > \chi _ { 0 } ^ { 2 } \right) = .10 \text { for } n = 10 \text {. }$

A random sample of 8 observations from an approximately normal distribution is shown below. 5 6 4 5 8 6 5 3 Find the observed level of significance for the test of $H _ { 0 } : \mu = 5$ against $H _ { \mathrm { a } } : \mu \neq 5$ . Interpret the result.

The value of $\beta$ is the area under the bell curve for the distribution of $\bar { x }$ centered at $\mu _ { \mathrm { a } }$ for values of $\bar { x }$ that fall within the acceptance region of the distribution of $\bar { x }$ centered at $\mu _ { 0 }$ .

Suppose we wish to test $H _ { 0 } : \mu = 39$ vs. $H _ { \mathrm { a } } : \mu < 39$ . Which of the following possible sample results gives the most evidence to support $H _ { \text {a } }$ (i.e., reject $H _ { 0 }$ )?

The alternative hypothesis is accepted as true unless there is overwhelming evidence that it is false.

Identify the observed level of significance for the test summarized on the screen below and interpret its value.

Statistics, Data, and Statistical Thinking

Methods for Describing Sets of Data

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics Available Online

Filters

Exam 8: Inferences Based on a Single

A __________ is a numerical quantity computed from the data of a sample and is used in reaching a decision on whether or not to reject the null hypothesis.

A random sample of 8 observations from an approximately normal distribution is shown below. 5 6 4 5 8 6 5 3 Find the observed level of significance for the test of H0:μ=5H _ { 0 } : \mu = 5H0​:μ=5 against Ha:μ≠5H _ { \mathrm { a } } : \mu \neq 5Ha​:μ=5 . Interpret the result.

The value of β\betaβ is the area under the bell curve for the distribution of xˉ\bar { x }xˉ centered at μa\mu _ { \mathrm { a } }μa​ for values of xˉ\bar { x }xˉ that fall within the acceptance region of the distribution of xˉ\bar { x }xˉ centered at μ0\mu _ { 0 }μ0​ .

Based on the information in the screen below, what would you conclude in the test of H0:μ≤14,Ha:μ>14. Use α=.01H_{0}: \mu \leq 14, H_{\mathrm{a}}: \mu>14 \text {. Use } \alpha=.01H0​:μ≤14,Ha​:μ>14. Use α=.01

Suppose we wish to test H0:μ=39H _ { 0 } : \mu = 39H0​:μ=39 vs. Ha:μ<39H _ { \mathrm { a } } : \mu < 39Ha​:μ<39 . Which of the following possible sample results gives the most evidence to support Ha H _ { \text {a } }Ha ​ (i.e., reject H0H _ { 0 }H0​ )?

The alternative hypothesis is accepted as true unless there is overwhelming evidence that it is false.

Identify the observed level of significance for the test summarized on the screen below and interpret its value.

Statistics, Data, and Statistical Thinking

Methods for Describing Sets of Data

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics Available Online

Filters

A random sample of 8 observations from an approximately normal distribution is shown below. 5 6 4 5 8 6 5 3 Find the observed level of significance for the test of $H _ { 0 } : \mu = 5$ against $H _ { \mathrm { a } } : \mu \neq 5$ . Interpret the result.

The value of $\beta$ is the area under the bell curve for the distribution of $\bar { x }$ centered at $\mu _ { \mathrm { a } }$ for values of $\bar { x }$ that fall within the acceptance region of the distribution of $\bar { x }$ centered at $\mu _ { 0 }$ .

Suppose we wish to test $H _ { 0 } : \mu = 39$ vs. $H _ { \mathrm { a } } : \mu < 39$ . Which of the following possible sample results gives the most evidence to support $H _ { \text {a } }$ (i.e., reject $H _ { 0 }$ )?