Question 1

Consider the following pairs of observations: $$\begin{array} { | c | c | c | c | c | c | } 
\hline x & 2 & 3 & 5 & 5 & 6 \
\hline y & 1.3 & 1.6 & 2.1 & 2.2 & 2.7 \
\hline
\end{array}$$ Find and interpret the value of the coefficient of correlation.

Accepted Answer

$$\begin{array} { l } 
S S _ { x y } = 45.1 - \frac { ( 21 ) ( 9.9 ) } { 5 } = 3.52 ; S S _ { x x } = 99 - \frac { ( 21 ) ^ { 2 } } { 5 } = 10.8 ; \
S S _ { y y } = 20.79 - \frac { ( 9.9 ) ^ { 2 } } { 5 } = 1.188 ; r = \frac { 3.52 } { \sqrt { 10.8 \cdot 1.188 } } \approx .9827 ;
\end{array}$$
There is a strong linear relationship between $x$ and $y$.

Question 2

Consider the following pairs of observations: $$\begin{array} { | c | c | c | c | c | c | } 
\hline x & 2 & 3 & 5 & 5 & 6 \
\hline y & 1.3 & 1.6 & 2.1 & 2.2 & 2.7 \
\hline
\end{array}$$ Find and interpret the value of the coefficient of determination.

Accepted Answer

$$S S _ { y y } = 1.188 ; S S E = .040741 ; r ^ { 2 } = 1 - \frac { .040741 } { 1.188 } \approx .9657 \text {; }$$
$96.57 \%$ of the sample variation in $y$ values can be attributed to the linear relationship between $x$ and $y$.

Question 3

A realtor collected the following data for a random sample of ten homes that recently sold
in her area. $$\begin{array} { | c | c | c | } 
\hline \text { House } & \text { Asking Price } & \text { Days on Market } \
\hline \mathrm { A } & \$ 114,500 & 29 \
\hline \mathrm { B } & \$ 149,900 & 16 \
\hline \mathrm { C } & \$ 154,700 & 59 \
\hline \mathrm { D } & \$ 159,900 & 42 \
\hline \mathrm { E } & \$ 160,000 & 72 \
\hline \mathrm { F } & \$ 165,900 & 45 \
\hline \mathrm { G } & \$ 169,700 & 12 \
\hline \mathrm { H } & \$ 171,900 & 39 \
\hline \mathrm { I } & \$ 175,000 & 81 \
\hline \mathrm { J } & \$ 289,900 & 121 \
\hline
\end{array}$$ a. Construct a scattergram for the data.
b. Find the least squares line for the data and plot the line on your scattergram.
c. Test whether the number of days on the market, y, is positively linearly related to the $$\text { asking price, } x \text {. Use } \alpha = .05 \text {. }$$

Accepted Answer

a.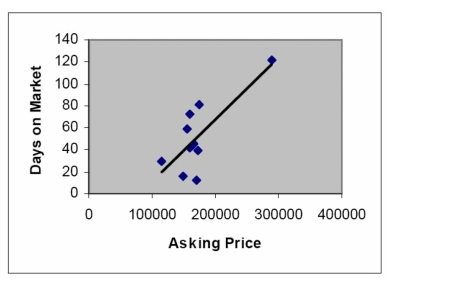

b. $S S _ { x y } = 10,232,660 ; S S _ { x x } \approx 1.833 \times 1010 ; \hat { \beta } _ { 1 } = .0005583 ; \bar { x } = 171,140$; $\bar { y } = 51.6 ; \hat { \beta } _ { 0 } = 51.6 - .0005583 ( 171,140 ) = - 43.94$
$\hat { y } = 43.94 + .0005583 x$
c. The test statistic is $\mathrm { t } = \frac { .0005583 } { 22.58 / \sqrt { 1.833 \times 10 ^ { 10 } } } \approx 3.35$.
Based on 8 degrees of freedom, the rejection region is $t > 1.860$. Since the test statistic falls in the rejection region, we reject the null hypothesis and conclude that the number of days on the market, $y$, is positively linearly related to the asking price, $x$.

Question 4

A study of the top 75 MBA programs attempted to predict the average starting salary (in $1000's) of graduates of the program based on the amount of tuition (in $1000's)charged by the program.
The results of a simple linear regression analysis are shown below: Least Squares Linear Regression of Salary
Predictor
$\begin{array} { l r c c l } \text { Variables } & \text { Coefficient } & \text { Std Error } & \text { T } & \text { P } \ \text { Constant } & 18.1849 & 10.3336 & 1.76 & 0.0826 \ \text { Size } & 1.47494 & 0.14017 & 10.52 & 0.0000 \end{array}$

In addition, we are told that the coefficient of correlation was calculated to be $r = 0.7763$. Interpret this result.

Accepted Answer

A)  There is a fairly strong negative linear relationship between the amount of tuition charged and the average starting salary variables. 
B)  There is a fairly strong positive linear relationship between the amount of tuition charged and the average starting salary variables. 
C)  There is almost no linear relationship between the amount of tuition charged and the average starting salary variables. 
D)  There is a very weak positive linear relationship between the amount of tuition charged and the average starting salary variables. 
A)  There is a fairly strong negative linear relationship between the amount of tuition charged and the average starting salary variables. 
B)  There is a fairly strong positive linear relationship between the amount of tuition charged and the average starting salary variables. 
C)  There is almost no linear relationship between the amount of tuition charged and the average starting salary variables. 
D)  There is a very weak positive linear relationship between the amount of tuition charged and the average starting salary variables.

Question 5

$$\text { Calculate SSE and } s ^ { 2 } \text { for } n = 30 , \mathrm { SS } _ { \mathrm { yy } } = 100 , \mathrm { SS } _ { \mathrm { xy } } = 60 \text {, and } \hat { \beta } 1 = .8 \text {. }$$

Accepted Answer

The answer of \[\text { Calculate SSE and } s...

Question 6

State the four basic assumptions about the general form of the probability distribution of
the random error ε.

Accepted Answer

Assumption 1: The mean of the probabilit

Question 7

The dean of the Business School at a small Florida college wishes to determine whether the grade-point average (GPA)of a graduating student can be used to predict the graduateʹs starting
Salary. More specifically, the dean wants to know whether higher GPAs lead to higher starting
Salaries. Records for 23 of last yearʹs Business School graduates are selected at random, and data
On GPA (x)and starting salary (y, in $thousands)for each graduate were used to fit the model $$E ( y ) = \beta _ { 0 } + \beta _ { 1 } x$$
The results of the simple linear regression are provided below.
$$\begin{array} { l l } 
\hat { y } = 4.25 + 2.75 x , & S S _ { x y } = 5.15 , S S _ { x x } = 1.87 \
S S y y = 15.17 , S S E = 1.0075
\end{array}$$
Calculate the value of $r ^ { 2 }$, the coefficient of determination.

Accepted Answer

A)  $0.339$ 
B)  $0.934$ 
C)  $0.872$ 
D)  $0.661$ 
A)  $0.339$ 
B)  $0.934$ 
C)  $0.872$ 
D)  $0.661$

Question 8

For the situation above, give a practical interpretation of $\mathrm { s } = 3213$.

Accepted Answer

A)  We estimate SALARY to increase $\$ 3,213$ for every 1-point increase in GMAT. 
B)  We expect to predict SALARY to within $2 ( 3213 ) = \$ 6,426$ of its true value using GMAT in a straight-line model. 
C)  Our predicted value of SALARY will equal $2 ( 3213 ) = \$ 6,426$ for any value of GMAT. 
D)  We expect the predicted SALARY to deviate from actual SALARY by at least $2 ( 3213 ) = \$ 6,426$ using GMAT in a straight-line model. 
A)  We estimate SALARY to increase $\$ 3,213$ for every 1-point increase in GMAT. 
B)  We expect to predict SALARY to within $2 ( 3213 ) = \$ 6,426$ of its true value using GMAT in a straight-line model. 
C)  Our predicted value of SALARY will equal $2 ( 3213 ) = \$ 6,426$ for any value of GMAT. 
D)  We expect the predicted SALARY to deviate from actual SALARY by at least $2 ( 3213 ) = \$ 6,426$ using GMAT in a straight-line model.

Question 9

For the situation above, give a practical interpretation of $r = .81$.

Accepted Answer

A)  We can predict SALARY correctly $81 \%$ of the time using GMAT in a straight-line model. 
B)  We estimate SALARY to increase $81 \%$ for every 1 -point increase in GMAT. 
C)  $81 \%$ of the sample variation in SALARY can be explained by using GMAT in a straight-line model. 
D)  There appears to be a positive correlation between SALARY and GMAT. 
A)  We can predict SALARY correctly $81 \%$ of the time using GMAT in a straight-line model. 
B)  We estimate SALARY to increase $81 \%$ for every 1 -point increase in GMAT. 
C)  $81 \%$ of the sample variation in SALARY can be explained by using GMAT in a straight-line model. 
D)  There appears to be a positive correlation between SALARY and GMAT.

Question 10

What is the relationship between diamond price and carat size? 307 diamonds were sampled and a straight-line relationship was hypothesized between y = diamond price (in dollars)and x = size of
The diamond (in carats). The simple linear regression for the analysis is shown below: Least Squares Linear Regression of PRICE
Predictor

Interpret the standard deviation of the regression model.

Accepted Answer

A)  We can explain $89.25 \%$ of the variation in the sampled diamond prices around their mean using the size of the diamond in a linear model. 
B)  For every 1-carat increase in the size of a diamond, we estimate that the price of the diamond will increase by $\$ 1117.56$. 
C)  We expect most of the sampled diamond prices to fall within $\$ 1117.56$ of their least squares predicted values. 
D)  We expect most of the sampled diamond prices to fall within $\$ 2235.12$ of their least squares predicted values. 
A)  We can explain $89.25 \%$ of the variation in the sampled diamond prices around their mean using the size of the diamond in a linear model. 
B)  For every 1-carat increase in the size of a diamond, we estimate that the price of the diamond will increase by $\$ 1117.56$. 
C)  We expect most of the sampled diamond prices to fall within $\$ 1117.56$ of their least squares predicted values. 
D)  We expect most of the sampled diamond prices to fall within $\$ 2235.12$ of their least squares predicted values.

Question 11

What is the relationship between diamond price and carat size? 307 diamonds were sampled and a straight-line relationship was hypothesized between y = diamond price (in dollars)and x = size of
The diamond (in carats). The simple linear regression for the analysis is shown below: Least Squares Linear Regression of PRICE
Predictor

Interpret the coefficient of determination for the regression model.

Accepted Answer

A)  There is sufficient evidence to indicate that the size of the diamond is a useful predictor of the price of a diamond when testing at alpha $= 0.05$. 
B)  For every 1-carat increase in the size of a diamond, we estimate that the price of the diamond will increase by $\$ 1117.56$. 
C)  We expect most of the sampled diamond prices to fall within $\$ 2235.12$ of their least squares predicted values. 
D)  We can explain $89.25 \%$ of the variation in the sampled diamond prices around their mean using the size of the diamond in a linear model. 
A)  There is sufficient evidence to indicate that the size of the diamond is a useful predictor of the price of a diamond when testing at alpha $= 0.05$. 
B)  For every 1-carat increase in the size of a diamond, we estimate that the price of the diamond will increase by $\$ 1117.56$. 
C)  We expect most of the sampled diamond prices to fall within $\$ 2235.12$ of their least squares predicted values. 
D)  We can explain $89.25 \%$ of the variation in the sampled diamond prices around their mean using the size of the diamond in a linear model.

Question 12

A county real estate appraiser wants to develop a statistical model to predict the appraised value of houses in a section of the county called East Meadow. One of the many variables thought to be
An important predictor of appraised value is the number of rooms in the house. Consequently, the
Appraiser decided to fit the simple linear regression model: $$E ( y ) = \beta _ { 0 } + \beta _ { 1 } x$$
where $y =$ appraised value of the house (in thousands of dollars) and $x =$ number of rooms. Using data collected for a sample of $n = 74$ houses in East Meadow, the following results were obtained:
$$y = 74.80 + 23.95 x$$
Give a practical interpretation of the estimate of the slope of the least squares line.

Accepted Answer

A)  For each additional dollar of appraised value, we estimate the number of rooms in the house to increase by $23.95$. 
B)  For a house with 0 rooms, we estimate the appraised value to be $\$ 74,800$. 
C)  For each additional room in the house, we estimate the appraised value to increase $\$ 74,800$. 
D)  For each additional room in the house, we estimate the appraised value to increase \$23,950. 
A)  For each additional dollar of appraised value, we estimate the number of rooms in the house to increase by $23.95$. 
B)  For a house with 0 rooms, we estimate the appraised value to be $\$ 74,800$. 
C)  For each additional room in the house, we estimate the appraised value to increase $\$ 74,800$. 
D)  For each additional room in the house, we estimate the appraised value to increase \$23,950.

Question 13

In a study of feeding behavior, zoologists recorded the number of grunts of a warthog
feeding by a lake in the 15 minute period following the addition of food. The data showing
the number of grunts and and the age of the warthog (in days)are listed below: $$\begin{array}{l}
\begin{array} { c c } 
\hline \text { Number of Grunts } & \text { Age (days) } \
\hline 83 & 118 \
61 & 134 \
32 & 148 \
37 & 153 \
56 & 160 \
33 & 167 \
55 & 176 \
10 & 182 \
13 & 188 \
\hline
\end{array}\
\text { Find and interpret the value of } r ^ { 2 } \text {. }
\end{array}$$

Accepted Answer

@#LAT-DLM& of the variation in

Question 14

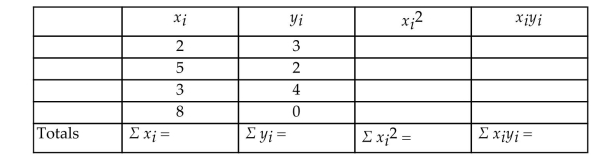a. Complete the table.

b. Find $S S _ { x y } , S S _ { x x } , \beta 1 , \bar { x } , \bar { y }$, and $\hat { \beta } _ { 0 }$.
c. Write the equation of the least squares line.

Accepted Answer

The answer of a. Complete the table.

b. Find...

Question 15

A company keeps extensive records on its new salespeople on the premise that sales
should increase with experience. A random sample of seven new salespeople produced
the data on experience and sales shown in the table. $\begin{array}{c|c}
\text { Months on Job } & \begin{array}{c}
\text { Monthly Sales } \
y \text { (\$ thousands) }
\end{array} \
\hline 2 & 2.4 \
4 & 7.0 \
8 & 11.3 \
12 & 15.0 \
1 & .8 \
5 & 3.7 \
9 & 12.0
\end{array}$

Summary statistics yield $S S _ { x x } = 94.8571 , S S _ { x y } = 124.7571 , S S _ { y y } = 176.5171 , \bar { x } = 5.8571$, and $\bar { y } = 7.4571$. Using $S S E = 12.435$, find and interpret the coefficient of determination.

Accepted Answer

@#LAT-DLM& 92.96% of the variation in th

Question 16

What is the relationship between diamond price and carat size? 307 diamonds were sampled and a straight-line relationship was hypothesized between y = diamond price (in dollars)and x = size of
The diamond (in carats). The simple linear regression for the analysis is shown below: Least Squares Linear Regression of PRICE
$\text { Predictor }$

The model was then used to create $95 \%$ confidence and prediction intervals for $\mathrm { y }$ and for E(Y) when the carat size of the diamond was 1 carat. The results are shown here:
$95 \%$ confidence interval for $\mathrm { E } ( \mathrm { Y } ) : ( \$ 9091.60 , \$ 9509.40 )$
$95 \%$ prediction interval for $Y : ( \$ 7091.50 , \$ 11,510.00 )$
Which of the following interpretations is correct if you want to use the model to estimate $E ( Y )$ for all 1 -carat diamonds?

Accepted Answer

A)  We are $95 \%$ confident that the price of a 1 -carat diamond will fall between $\$ 7091.50$ and $\$ 11,510.00$. 
B)  We are $95 \%$ confident that the average price of all 1 -carat diamonds will fall between $\$ 9091.60$ and $\$ 9509.40$. 
C)  We are $95 \%$ confident that the average price of all 1 -carat diamonds will fall between $\$ 7091.50$ and $\$ 11,510.00$. 
D)  We are $95 \%$ confident that the price of a 1-carat diamond will fall between $\$ 9091.60$ and $\$ 9509.40$. 
A)  We are $95 \%$ confident that the price of a 1 -carat diamond will fall between $\$ 7091.50$ and $\$ 11,510.00$. 
B)  We are $95 \%$ confident that the average price of all 1 -carat diamonds will fall between $\$ 9091.60$ and $\$ 9509.40$. 
C)  We are $95 \%$ confident that the average price of all 1 -carat diamonds will fall between $\$ 7091.50$ and $\$ 11,510.00$. 
D)  We are $95 \%$ confident that the price of a 1-carat diamond will fall between $\$ 9091.60$ and $\$ 9509.40$.

Question 17

In team-teaching, two or more teachers lead a class. A researcher tested the use of 74)
team-teaching in mathematics education. Two of the variables measured on each teacher
in a sample of 159 mathematics teachers were years of teaching experience x and reported
success rate y (measured as a percentage)of team-teaching mathematics classes.
The correlation coefficient for the sample data was reported as r = -0.3. Interpret this
result.

Accepted Answer

There is a weak negative corre

Question 18

An academic advisor wants to predict the typical starting salary of a graduate at a top business school using the GMAT score of the school as a predictor variable. A simple linear regression of
SALARY versus GMAT using 25 data points is shown below. $$\hat { \beta _ { 0 } } = - 92040 \hat { \beta } 1 = 228 s = 3213 r ^ { 2 } = .66 r = .81 \quad \mathrm { df } = 23 \quad t = 6.67$$
Give a practical interpretation of $r ^ { 2 } = .66$.

Accepted Answer

A)  $66 \%$ of the sample variation in SALARY can be explained by using GMAT in a straight -line model. 
B)  We can predict SALARY correctly $66 \%$ of the time using GMAT in a straight-line model. 
C)  We estimate SALARY to increase $\$ .66$ for every 1 -point increase in GMAT. 
D)  We expect to predict SALARY to within $2 [ \sqrt { .66 } ]$ of its true value using GMAT in a straight-line model. 
A)  $66 \%$ of the sample variation in SALARY can be explained by using GMAT in a straight -line model. 
B)  We can predict SALARY correctly $66 \%$ of the time using GMAT in a straight-line model. 
C)  We estimate SALARY to increase $\$ .66$ for every 1 -point increase in GMAT. 
D)  We expect to predict SALARY to within $2 [ \sqrt { .66 } ]$ of its true value using GMAT in a straight-line model.

Question 19

Is the number of games won by a major league baseball team in a season related to the
teamʹs batting average? Data from 14 teams were collected and the summary statistics
yield: $\sum y = 1,134 , \sum ^ { x } = 3.642 , \sum y ^ { 2 } = 93,110 , \sum ^ { x ^ { 2 } } = .948622$, and $\sum ^ { x y } = 295.54$
Assume $\hat { \beta } 1 = 455.27$ and $\hat { \sigma } = 9.18$. Conduct a test of hypothesis to determine if a positive linear relationship exists between team batting average and number of wins. Use $\alpha = .05$.

Accepted Answer

We test: @#LAT-DLM&
@#LAT-DLM&
The test statistic is @#LAT-DLM&.
\[\be

Question 20

Consider the following pairs of observations: $\begin{array}{|c|c|c|c|c|c|}
\hline x & 2 & 3 & 5 & 5 & 6 \
\hline y & 1.3 & 1.6 & 2.1 & 2.2 & 2.7 \
\hline
\end{array}$

a. Construct a scattergram for the data. Does the scattergram suggest that $y$ is positively linearly related to $x$ ?
b. Find the slope of the least squares line for the data and test whether the data provide sufficient evidence that $y$ is positively linearly related to $x$. Use $\alpha = .05$.

Accepted Answer

a. @#IMG-DLM&
The scattergram does suggest that @#LAT-DLM& i

Consider the following pairs of observations: x 2 3 5 5 6 y 1.3 1.6 2.1 2.2 2.7 Find and interpret the value of the coefficient of correlation.

Consider the following pairs of observations: x 2 3 5 5 6 y 1.3 1.6 2.1 2.2 2.7 Find and interpret the value of the coefficient of determination.

$\text { Calculate SSE and } s ^ { 2 } \text { for } n = 30 , \mathrm { SS } _ { \mathrm { yy } } = 100 , \mathrm { SS } _ { \mathrm { xy } } = 60 \text {, and } \hat { \beta } 1 = .8 \text {. }$

State the four basic assumptions about the general form of the probability distribution of the random error ε.

For the situation above, give a practical interpretation of $\mathrm { s } = 3213$ .

For the situation above, give a practical interpretation of $r = .81$ .

Statistics, Data, and Statistical Thinking

Methods for Describing Sets of Data

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single

Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics Available Online

Filters

Exam 11: Simple Linear Regression