Exam 8: Inferences Based on a Single
Exam 1: Statistics, Data, and Statistical Thinking77 Questions
Exam 2: Methods for Describing Sets of Data187 Questions
Exam 3: Probability284 Questions
Exam 4: Discrete Random Variables134 Questions
Exam 5: Continuous Random Variables138 Questions
Exam 6: Sampling Distributions52 Questions
Exam 7: Inferences Based on a Single Sample: Estimation With Confidence Intervals125 Questions
Exam 8: Inferences Based on a Single144 Questions
Exam 9: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses100 Questions
Exam 10: Analysis of Variance: Comparing More Than Two Means91 Questions
Exam 11: Simple Linear Regression113 Questions
Exam 12: Multiple Regression and Model Building131 Questions
Exam 13: Categorical Data Analysis60 Questions
Exam 14: Nonparametric Statistics Available Online87 Questions
Select questions type
Solve the problem.
-How many tissues should a package of tissues contain? Researchers have determined that a person uses an average of 68 tissues during a cold. Suppose a random sample of 10,000 people yielded the following data on the number of tissues used during a cold: . Using the sample information provided, set up the calculation for the test statistic for the relevant hypothesis test, but do not simplify.
(Multiple Choice)
4.8/5  (36)
(36)
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
-z < -1.96 or z > 1.96
(Essay)
4.9/5  (30)
(30)
It is desired to test against using . The population in question is uniformly distributed with a standard deviation of 15 . A random sample of 49 will be drawn from this population. If is really equal to 50 , what is the power of this test?
(Multiple Choice)
4.7/5  (35)
(35)
In a test of against , the sample data yielded the test statistic . Find and interpret the -value for the test.
(Essay)
4.9/5  (34)
(34)
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
-z < -1.96
(Essay)
4.9/5  (32)
(32)
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X
 What assumptions are necessary for any inferences derived from this printout to be valid?
What assumptions are necessary for any inferences derived from this printout to be valid?
(Multiple Choice)
4.8/5  (38)
(38)
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the university's students differed from 20 minutes. Find the large-sample rejection region for the test of interest to the college when using a level of significance of .
(Multiple Choice)
4.8/5  (37)
(37)
Suppose we wish to test vs. . What will result if we conclude that the mean is greater than 43 when its true value is really 45 ?
(Multiple Choice)
4.9/5  (35)
(35)
For the given binomial sample size and null-hypothesized value of determine whether the sample size is large
enough to use the normal approximation methodology to conduct a test of the null hypothesis
-
(Multiple Choice)
4.9/5  (42)
(42)
A sample of 6 measurements, randomly selected from a normally distributed population, resulted in the following summary statistics: . Test the null hypothesis that the mean of the population is 10 against the alternative hypothesis . Use .
(Essay)
4.8/5  (44)
(44)
Consider a test of performed with the computer. SPSS reports a two-tailed p-value of 0.2112. Make the appropriate conclusion for the given situation:
(Multiple Choice)
4.7/5  (36)
(36)
A national organization has been working with utilities throughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 18 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. Based on a sample of wind speed recordings (taken at random intervals), the wind speed at the site averaged , with a standard deviation of . To determine whether the site meets the organization's requirements, consider the test, vs. , where is the true mean wind speed at the site and . Fill in the blanks. "A Type I error in the context of this problem is to conclude that the true mean wind speed at the site ________ when it actually ______
(Multiple Choice)
4.9/5  (33)
(33)
The owner of Get-A-Away Travel has recently surveyed a random sample of 444 customers to determine whether the mean age of the agency's customers is over 33 . The appropriate hypotheses are . If he concludes the mean age is over 33 when it is not, he makes a _______error. If he concludes the mean age is not over 33 when it is, he makes a ______error.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The State Association of Retired Teachers has recently taken flak from some of its members regarding the poor choice of the association's name. The association's by-laws require that more than 60 percent of the association must approve a name change. Rather than convene a meeting, it is first desired to use a sample to determine if meeting is necessary. Identify the null and alternative hypothesis that should be tested to determine if a name change is warranted.
(Multiple Choice)
4.8/5  (31)
(31)
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they
Spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis.
The goal was to determine if the average travel time of all the universityʹs students differed from
20 minutes. Suppose the sample mean and sample standard deviation were calculated to be 23.2
And 20.26 minutes, respectively. Calculate the value of the test statistic to be used in the test.
(Multiple Choice)
4.9/5  (40)
(40)
A random sample of observations, selected from a normal population, is used to test the null hypothesis . Specify the appropriate rejection region.
(Multiple Choice)
4.8/5  (39)
(39)
Based on the information in the screen below, what would you conclude in the test of
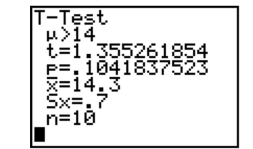
(Essay)
4.9/5  (34)
(34)
It is desired to test against using . The population in question is uniformly distributed with a standard deviation of . A random sample of 100 will be drawn from this population. If is really equal to , what is the value of associated with this test?
(Multiple Choice)
4.8/5  (37)
(37)
A random sample of observations is selected from a normal population to test against at . Specify the rejection region.
(Essay)
5.0/5  (44)
(44)
Showing 121 - 140 of 144
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)