Exam 6: Normal Probability Distributions

Solve the problem. -A bank's loan officer rates applicants for credit. The ratings are normally distributed with a mean of 200 and a standard deviation of 50 . Find $\mathrm { P } _ { 6 }$ , the score which separates the lower $60 \%$ from the top $40 \%$ .

Using the following uniform density curve, answer the question. 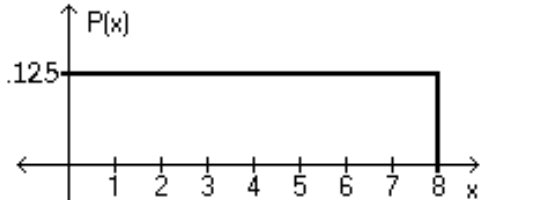-What is the probability that the random variable has a value less than 6?

Provide an appropriate response. -Describe the process for finding x values given probabilities.

The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of 0°C at the freezing point of water. Tests on a large sample of these thermometers reveal that at the freezing point of water, some give readings below 0°C (denoted by negative numbers) and some give readings above 0°C (denoted by positive numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is 1.00°C. Also assume that the frequency distribution of errors closely resembles the normal distribution. A thermometer is randomly selected and tested. Find the temperature reading corresponding to the given information. -A quality control analyst wants to examine thermometers that give readings in the bottom 4%. Find the reading that separates the bottom 4% from the others.

In one region, the September energy consumption levels for single-family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. For a randomly selected home, find the probability that the September energy consumption level is between 1100 kWh and 1225 kWh.

Assume that X has a normal distribution, and find the indicated probability. -The mean is $\boldsymbol { \mu } = 137.0$ and the standard deviation is $\boldsymbol { \sigma } = 5.3$ . Find the probability that $X$ is between $134.4$ and 140.1.

Solve the problem. -In a population of 240 women, the heights of the women are normally distributed with a mean of $64.2$ inches and a standard deviation of $3.2$ inches. If 36 women are selected at random, find the mean $\mu _ { \mathrm { x } } ^ { - }$ and standard deviation $\sigma _ { \mathrm { x } } ^ { - }$ of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.

Solve the problem. -Assume that $\mathrm { z }$ scores are normally distributed with a mean of 0 and a standard deviation of 1 . If $\mathrm { P } ( - \mathrm { a } < \mathrm { z } < \mathrm { a } ) = 0.4314$ , find $\mathrm { a }$ .

For the binomial distribution with the given values for n and p -The probability that the number of correct answers is between 16 and 38 inclusive

Solve the problem. -A final exam in Math 160 has a mean of 73 with standard deviation 7.8. If 24 students are randomly selected, find the probability that the mean of their test scores is greater than 71.

Solve the problem. -For women aged 18-24, systolic blood pressures (in mm Hg)are normally distributed with a mean of 114.8 and a standard deviation of 13.1. If 36 women are selected at random from a population of 300 women aged 18-24, find the probability that their mean systolic blood pressure will be less than 110 mm Hg. Assume that the sampling is done without replacement and use a finite population correction factor with N = 300.

Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution. -In one county, the conviction rate for speeding is 85%. Estimate the probability that of the next 100 speeding summonses issued, there will be at least 90 convictions.

Solve the problem. -Suppose that replacement times for washing machines are normally distributed with a mean of 9.3 years and a standard deviation of 1.1 years. Find the probability that 70 randomly selected washing machines will have a mean replacement time less than 9.1 years.

For the binomial distribution with the given values for n and p -n = 18 and p = .6

The systolic blood pressures of the patients at a hospital are normally distributed with a mean of 136 mm Hg and a standard deviation of 13.8 mm Hg. Find the two blood pressures having these properties: the mean is midway between them and 90% of all blood pressures are between them.

A baseball player has a batting average of 0.346, so the probability of a hit is 0.346. Assume that his hitting attempts are independent of each other. Assume that the batter gets up to bat 4 times in each game. Estimate the probability that in 50 consecutive games, there are at least 45 games in which the batter gets at least one hit. (Hint: first find the probability that in one game the batter gets at least one hit)

Construct a normal probability plot of the given data. Use your plot to determine whether the data come from a normally distributed population -The systolic blood pressure (in mmHg)is given below for a sample of 12 men aged between 60 and 65. 127 135 118 164 143 130 125 153 120 173 140 180

Solve the problem. -The amount of snowfall falling in a certain mountain range is normally distributed with a mean of 74 inches, and a standard deviation of 12 inches. What is the probability that the mean annual snowfall during 36 randomly picked years will exceed 76.8 inches?

Using the following uniform density curve, answer the question. -What is the probability that the random variable has a value greater than 5.3?

Provide an appropriate response. -Describe the process for finding probabilities using z scores and the standard normal distribution. Give an example to support your description.