Exam 6: Normal Probability Distributions
Exam 1: Introduction to Statistics85 Questions
Exam 2: Summarizing and Graphing Data82 Questions
Exam 3: Statistics for Describing, Exploring, and Comparing Data149 Questions
Exam 4: Probability170 Questions
Exam 5: Probability Distributions158 Questions
Exam 6: Normal Probability Distributions173 Questions
Exam 7: Estimates and Sample Sizes139 Questions
Exam 8: Hypothesis Testing130 Questions
Exam 9: Inferences From Two Samples105 Questions
Exam 10: Correlation and Regression129 Questions
Exam 11: Multinomial Experiments and Contingency Tables31 Questions
Exam 12: Analysis of Variance60 Questions
Exam 13: Nonparametric Statistics64 Questions
Exam 14: Statistical Process Control38 Questions
Select questions type
Solve the problem.
-The scores on a certain test are normally distributed with a mean score of 51 and a standard deviation of 2. What is the probability that a sample of 90 students will have a mean score of at least 51.2108?
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-In one region, the September energy consumption levels for single-family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. Find P45, which is the consumption level separating the bottom 45% from the top 55%.
(Multiple Choice)
4.8/5  (36)
(36)
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.
-A multiple choice test consists of 60 questions. Each question has 4 possible answers of which one is correct. If all answers are random guesses, estimate the probability of getting at least 20% correct.
(Multiple Choice)
4.7/5  (33)
(33)
Provide an appropriate response.
-Describe the difference between z scores and area scores. Show each score's relationship to the graph of the standard normal distribution and discuss the possible sign values for each score.
(Essay)
4.7/5  (25)
(25)
Scores on a test are normally distributed with a mean of 68.2 and a standard deviation of 10.4. Estimate the probability that among 75 randomly selected students, at least 20 of them score greater than 78.
(Multiple Choice)
4.7/5  (32)
(32)
Solve the problem.
-Human body temperatures are normally distributed with a mean of 98.20°F and a standard deviation of 0.62°F. If 19 people are randomly selected, find the probability that their mean body temperature will be less than 98.50°F.
(Multiple Choice)
4.9/5  (45)
(45)
Construct a normal probability plot of the given data. Use your plot to determine whether the data come from a normally distributed population
-The numbers obtained on 50 rolls of a die. 1 5 5 3 6 4 5 6 3 4 2 5 3 5 4 2 1 4 3 1 6 1 2 6 1 2 5 3 3 4 4 1 3 1 6 2 2 5 5 3 3 5 1 6 2 1 1 4 6 5
(Essay)
4.7/5  (35)
(35)
Provide an appropriate response.
-State the Central Limit theorem. Describe the sampling distribution for a population that is uniform and for a population that is normal.
(Essay)
4.9/5  (38)
(38)
Solve the problem.
-Assume that women's heights are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. If 90 women are randomly selected, find the probability that they have a mean height between 62.9 inches and 64.0 inches.
(Multiple Choice)
4.9/5  (31)
(31)
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.
-Two percent of hair dryers produced in a certain plant are defective. Estimate the probability that of 10,000 randomly selected hair dryers, exactly 225 are defective.
(Multiple Choice)
4.7/5  (37)
(37)
Assume that the weight loss for the first month of a diet program varies between 6 pounds and 12 pounds, and is spread evenly over the range of possibilities, so that there is a uniform distribution. Find the probability of the given range of pounds lost
-More than 9 pounds
(Multiple Choice)
4.8/5  (34)
(34)
A poll of 1300 randomly selected students in grades 6 through 8 was conducted and found that 44% enjoy playing sports. Is the 44% result a statistic or a parameter? Explain.
(Essay)
4.9/5  (42)
(42)
Solve the problem.
-The serum cholesterol levels for men in one age group are normally distributed with a mean of 178.1 and a standard deviation of 40.7. All units are in mg/100 mL. Find the two levels that separate the top 9% and the bottom 9%.
(Multiple Choice)
5.0/5  (43)
(43)
The lengths of human pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. What is the probability that a pregnancy lasts at least 300 days?
(Multiple Choice)
4.7/5  (42)
(42)
Use the continuity correction and describe the region of the normal curve that corresponds to the indicated binomial probability.
-The probability of no more than 71 defective CD's
(Multiple Choice)
4.8/5  (34)
(34)
Merta reports that 74% of its trains are on time. A check of 60 randomly selected trains shows that 38 of them arrived on time. Find the probability that among the 60 trains, 38 or fewer arrive on time. Based on the result, does it seem plausible that the "on-time" rate of 74% could be correct?
(Multiple Choice)
4.8/5  (38)
(38)
A normal probability plot is given below for the lifetimes (in hours)of a sample of batteries of a particular brand. Use the plot to assess the normality of the lifetimes of these batteries. Explain your reasoning. 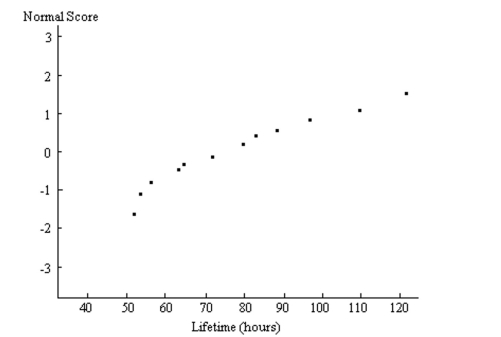
(Essay)
4.8/5  (41)
(41)
Assume that the weights of quarters are normally distributed with a mean of 5.67 g and a standard deviation 0.070 g. A vending machine will only accept coins weighing between 5.48 g and 5.82 g. What percentage of legal quarters will be rejected?
(Multiple Choice)
4.7/5  (38)
(38)
A normal probability plot is given below for the weekly incomes (in dollars)of a sample of engineers in one town. Use the plot to assess the normality of the incomes of engineers in this town. Explain your reasoning. 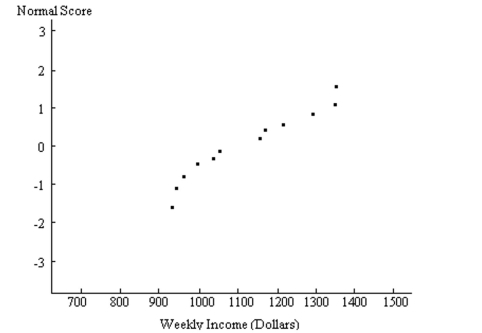
(Essay)
4.9/5  (36)
(36)
Solve the problem.
-Scores on an English test are normally distributed with a mean of 33.8 and a standard deviation of 8.5. Find the score that separates the top 59% from the bottom 41%
(Multiple Choice)
4.9/5  (37)
(37)
Showing 121 - 140 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)