Exam 2: Acute Angles and Right Triangles
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Find the sign of the following.
-cot (ϴ + 180°), given that ϴ is in the interval (270°, 360°).
(Multiple Choice)
4.9/5  (44)
(44)
Determine whether the statement is true or false.
-cos 195° = 2 cos 225° cos 30° + 2 sin 225° sin 30°
(True/False)
4.8/5  (38)
(38)
Find the sign of the following.
-cos (ϴ + 180°), given that ϴ is in the interval (90°, 180°).
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-A 5.6-ft fence is 12.818 ft away from a plant in the direction of the sun. It is observed that the shadow of the fence extends exactly to the bottom of the plant. (See drawing)Find ϴ, the angle of
Elevation of the sun at that time. Round the measure of the angle to the nearest tenth of a degree
When necessary. 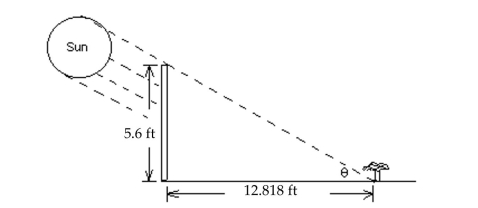
(Multiple Choice)
4.9/5  (41)
(41)
Determine whether the statement is true or false.
-cos 30° + cos 45° = cos 75°
(True/False)
4.9/5  (39)
(39)
Solve the problem.
-Bob is driving along a straight and level road straight toward a mountain. At some point on his trip he measures the angle of elevation to the top of the mountain and finds it to be 21° 32´. He then
Drives 1 mile (1 mile = 5280 ft)more and measures the angle of elevation to be 35° 7´. Find the
Height of the mountain to the nearest foot.
(Multiple Choice)
4.7/5  (32)
(32)
Solve the right triangle.
-
Round values to one decimal place.
(Multiple Choice)
4.9/5  (37)
(37)
Use a calculator to decide whether the statement is true or false.
-
(Multiple Choice)
4.9/5  (34)
(34)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and
(Multiple Choice)
4.8/5  (33)
(33)
Use a calculator to decide whether the statement is true or false.
-sin (150° + 30°)= sin 150° + sin 30°
(True/False)
4.7/5  (38)
(38)
Solve the problem.
-If an automobile is traveling at velocity (in feet per second), the safe radius for a curve with superelevation is given by the formula , where and are constants. A road is being constructed for automobiles traveling at 50 miles per hour. If , and , calculate R. Round to the nearest foot. (Hint: 1 mile feet)
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-In one area, the lowest angle of elevation of the sun in winter is 29° 8´. Find the minimum distance x that a plant needing full sun can be placed from a fence that is 5 feet high. Round your answer to
The tenths place when necessary. 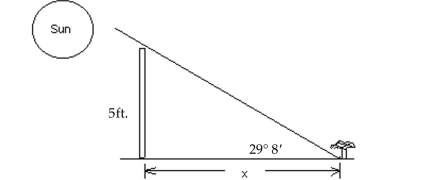
(Multiple Choice)
4.7/5  (46)
(46)
Solve the right triangle.
-B = 25.9°, c = 4.1 mm, C = 90° Round values to one decimal place.
(Multiple Choice)
4.7/5  (33)
(33)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and
(Multiple Choice)
4.9/5  (42)
(42)
Without using a calculator, give the exact trigonometric function value with rational denominator.
-sin 60°
(Multiple Choice)
4.8/5  (36)
(36)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-cos 39° 5' cos 50° 55' - sin 39° 5' sin 50° 55'
(Multiple Choice)
4.8/5  (45)
(45)
Evaluate the function requested. Write your answer as a fraction in lowest terms.
-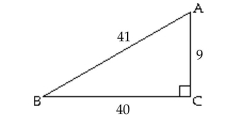 Find .
Find .
(Multiple Choice)
4.8/5  (44)
(44)
Showing 61 - 80 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)