Exam 2: Acute Angles and Right Triangles
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Write the function in terms of its cofunction. Assume that any angle in which an unknown appears is an acute angle.
-tan 41°
(Multiple Choice)
4.8/5  (42)
(42)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-sin (-34°20´)
(Multiple Choice)
5.0/5  (39)
(39)
Solve the right triangle.
-A = 72° 6´, c = 278 m , C = 90° Round side lengths to two decimal places, if necessary.
(Multiple Choice)
4.9/5  (34)
(34)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-2 sin 44° 14' cos 44° 14' - sin 88° 28'
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-In one area, the lowest angle of elevation of the sun in winter is 21° 7´. A fence is to be built 12.4 ft away from a plant in the direction of the sun. (See drawing)Find the maximum height, x , for the
Fence so that the plant will get full sun. Round your answer to the tenths place when necessary. 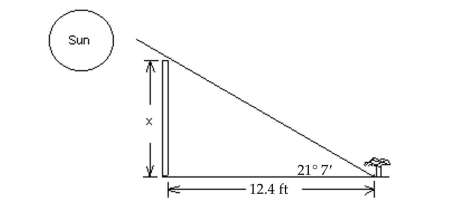
(Multiple Choice)
4.7/5  (38)
(38)
Find all values of , if is in the interval [0, 360°) and has the given function value.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-On a sunny day, a tree and its shadow form the sides of a right triangle. If the hypotenuse is 40 meters long and the tree is 32 meters tall, how long is the shadow?
(Multiple Choice)
5.0/5  (38)
(38)
Solve the problem.
-When sitting atop a tree and looking down at his pal Joey, the angle of depression of Mack's line of sight is 51°11'. If Joey is known to be standing 32 feet from the base of the tree, how tall is the tree
(to the nearest foot)?
(Multiple Choice)
4.9/5  (39)
(39)
Use a calculator to decide whether the statement is true or false.
-sin (2 ·30°)= 2 · sin 30°
(True/False)
4.8/5  (39)
(39)
Solve the problem.
-A tunnel is to be dug from point A to point B. Both A and B are visible from point C. If AC is 235 miles and BC is 625 miles, and if angle C is 90°, find the measure of angle B. Round your answer to
The tenths place.
(Multiple Choice)
4.7/5  (32)
(32)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-csc 30°5´
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-Snell's Law states that . Use this law to find the requested value. If , , and , find .
(Multiple Choice)
4.8/5  (43)
(43)
Find the sign of the following.
-sec (-ϴ), given that ϴ is in the interval (180°, 270°).
(Multiple Choice)
4.9/5  (36)
(36)
Write the function in terms of its cofunction. Assume that any angle in which an unknown appears is an acute angle.
-sec 29.7°
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A formula used by an engineer to determine the safe radius of a curve, , when designing a road is: , where is the superelevation of the road and is the velocity (in feet per second) for which the curve is designed. If per , and , find . Round to the nearest foot.
(Multiple Choice)
4.9/5  (36)
(36)
An observer for a radar station is located at the origin of a coordinate system. For the point given, find the bearing of an
airplane located at that point. Express the bearing using both methods.
-( , 0)
(Multiple Choice)
4.8/5  (36)
(36)
Use a calculator to decide whether the statement is true or false.
-sin (180°+ 225°)= sin 180° · cos 225° + cos 180° · sin 225°
(True/False)
4.8/5  (32)
(32)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-Radio direction finders are set up at points A and B, 8.68 mi apart on an east-west line. From A it is found that the bearing of a signal from a transmitter is N 54.3°E, while from B it is N 35.7°W. Find
The distance of the transmitter from B, to the nearest hundredth of a mile.
(Multiple Choice)
4.8/5  (36)
(36)
Solve the right triangle. If two sides are given, give angles in degrees and minutes.
-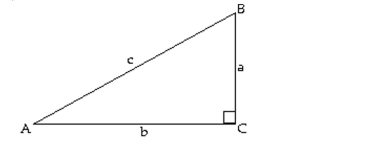 Round side lengths to one decimal place.
Round side lengths to one decimal place.
(Multiple Choice)
4.7/5  (45)
(45)
Showing 181 - 200 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)