Exam 2: Acute Angles and Right Triangles
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-From a balloon 1037 feet high, the angle of depression to the ranger headquarters is 58°41'. How far is the headquarters from a point on the ground directly below the balloon (to the nearest foot)?
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Find a formula for the area of the figure in terms of s. 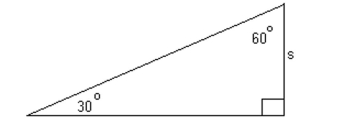
(Multiple Choice)
4.8/5  (35)
(35)
Find a solution for the equation. Assume that all angles are acute angles.
-sin A = cos 8A
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-A person is watching a car from the top of a building. The car is traveling on a straight road directly toward the building. When first noticed, the angle of depression to the car is 26° 53´. When the car
Stops, the angle of depression is 42° 31´. The building is 240 feet tall. How far did the car travel from
When it was first noticed until it stopped? Round to the nearest foot.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem for the given information.
-Find the equation of a line passing through the origin so that the cosine of the angle between the line in quadrant and the positive -axis is .
(Multiple Choice)
4.9/5  (28)
(28)
Evaluate the function requested. Write your answer as a fraction in lowest terms.
-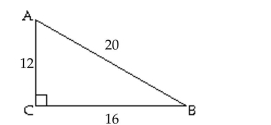 Find .
Find .
(Multiple Choice)
4.7/5  (39)
(39)
Solve the problem.
-Any offset between a stationary radar gun and a moving target creates a "cosine effect" that reduces the radar mileage reading by the cosine of the angle between the gun and the vehicle. That is, the
Radar speed reading is the product of the actual reading and the cosine of the angle. Find the radar
Reading to the nearest hundredth for the auto shown in the figure. 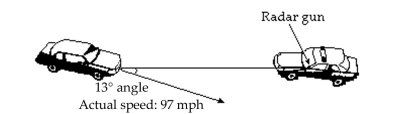
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A person is watching a boat from the top of a lighthouse. The boat is approaching the lighthouse directly. When first noticed, the angle of depression to the boat is 13° 12´. When the boat stops, the
Angle of depression is 49° 49´. The lighthouse is 200 feet tall. How far did the boat travel from when
It was first noticed until it stopped? Round to the nearest foot.
(Multiple Choice)
4.8/5  (44)
(44)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-sin 304°53´
(Multiple Choice)
4.8/5  (35)
(35)
Without using a calculator, give the exact trigonometric function value with rational denominator.
-cos 60°
(Multiple Choice)
4.8/5  (36)
(36)
Find a solution for the equation. Assume that all angles are acute angles.
-
(Multiple Choice)
4.7/5  (36)
(36)
The number represents an approximate measurement. State the range represented by the measurement.
-21 ft
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Find the exact value of x in the figure. 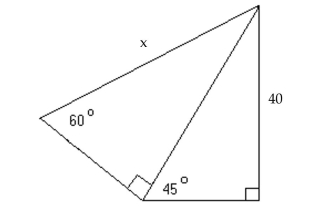
(Multiple Choice)
4.7/5  (37)
(37)
Evaluate the function requested. Write your answer as a fraction in lowest terms.
-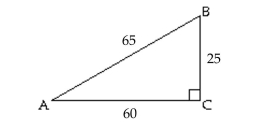 Find .
Find .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A 37-foot ladder is leaning against the side of a building. If the ladder makes an angle of 24° 16´ with the side of the building, how far up from the ground does the ladder make contact with
The building? Round your answer to the hundredths place when necessary.
(Multiple Choice)
4.9/5  (37)
(37)
Find a value of in [0°, 90°] that satisfies the statement. Leave answer in decimal degrees rounded to seven decimal
places, if necessary.
-sin ϴ = 0.81107642
(Multiple Choice)
4.7/5  (31)
(31)
Solve the problem.
-Snell's Law states that . Use this law to find the requested value. If , , find . Round your answer to the nearest degree.
(Multiple Choice)
4.8/5  (36)
(36)
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary.
-
(Multiple Choice)
4.9/5  (27)
(27)
Showing 21 - 40 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)