Exam 2: Acute Angles and Right Triangles
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-In 1838, the German mathematician and astronomer Friedrich Wilhelm Bessel was the first person to calculate the distance to a star other than the Sun. He accomplished this by first determining the parallax of the star, 61 Cygni, at arc seconds (Parallax is the change in position of the star measured against background stars as Earth orbits the Sun. See illustration.) If the distance from Earth to the Sun is about and seconds minutes degrees, determine the distance d from Earth to 61 Cygni using Bessel's figures. Express the answer in scientific notation.
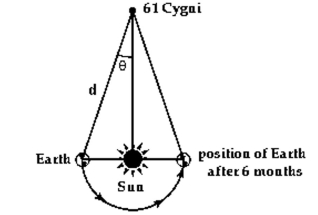
(Multiple Choice)
4.9/5  (33)
(33)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and .
(Multiple Choice)
4.7/5  (39)
(39)
Find a value of in [0°, 90°] that satisfies the statement. Leave answer in decimal degrees rounded to seven decimal
places, if necessary.
-cot ϴ = 1.7009187
(Multiple Choice)
4.7/5  (28)
(28)
Decide whether the statement is true or false.
-sin 86° > sin 24°
(True/False)
4.8/5  (33)
(33)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and .
(Multiple Choice)
4.8/5  (33)
(33)
Write the function in terms of its cofunction. Assume that any angle in which an unknown appears is an acute angle.
-cos 31.2°
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-A conservation officer needs to know the width of a river in order to set instruments correctly for a study of pollutants in the river. From point A, the conservation officer walks 100 feet downstream
And sights point B on the opposite bank to determine that ϴ = 30° (see figure). How wide is the river
(round to the nearest foot)? 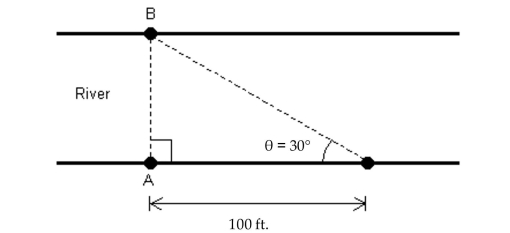
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-A person is watching a car from the top of a building. The car is traveling on a straight road away from the building. When first noticed, the angle of depression to the car is 45° 56´. When the car
Stops, the angle of depression is 22° 34´. The building is 270 feet tall. How far did the car travel from
When it was first noticed until it stopped? Round to the nearest foot.
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-The grade resistance F of a car traveling up or down a hill is modeled by the equation F = W sin ϴ where W is the weight of the car and ϴ is the angle of the hill's grade (ϴ > 0 for uphill travel, ϴ < 0
For downhill travel). What is the grade resistance (to the nearest pound)of a 3000-lb car traveling
Uphill on a 3° grade (ϴ = 3°)?
(Multiple Choice)
4.8/5  (39)
(39)
Find all values of , if is in the interval [0, 360°) and has the given function value.
- is undefined
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem for the given information.
-Find the equation of a line passing through the origin so that the cosine of the angle between the line in quadrant and the positive -axis is .
(Multiple Choice)
4.9/5  (43)
(43)
Determine whether the statement is true or false.
-sin 120° = 2 sin 60° cos 60°
(True/False)
4.8/5  (37)
(37)
Solve the problem.
-The length of the base of an isosceles triangle is 33.28 meters. Each base angle is 37.57°. Find the length of each of the two equal sides of the triangle. Round your answer to the hundredths place.
(Multiple Choice)
4.7/5  (45)
(45)
Find a value of in [0°, 90°] that satisfies the statement. Leave answer in decimal degrees rounded to seven decimal
places, if necessary.
-sec ϴ = 2.7259498
(Multiple Choice)
4.9/5  (35)
(35)
Showing 41 - 60 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)