Exam 10: Analytic Geometry in Three Dimensions
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Find a unit vector orthogonal to and .
leadcoeff(a)i leadcoeff(d)
(Multiple Choice)
4.8/5  (30)
(30)
Find a set of symmetric equations of the line that passes through the points and
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the parallelpiped with the given vertices.
(Multiple Choice)
4.8/5  (29)
(29)
Find the area of the parallelogram that has the vectors as adjacent sides.
(Multiple Choice)
4.8/5  (33)
(33)
For the points :
a. Verify that the points are vertices of a parallelogram. Show all work.
b. Find the area of the parallelogram. Show all work.
c. Determine whether the parallelogram is a rectangle.
(Essay)
4.8/5  (38)
(38)
Use the scalar triple product to find the volume of the parallelepiped having adjacent edges , and .
(Multiple Choice)
4.8/5  (37)
(37)
Find the general form of the equation of the plane passing through the three points. [Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.]
(Multiple Choice)
4.7/5  (33)
(33)
Find the magnitude of the vector described below.
Initial point:
Terminal point:
(Multiple Choice)
4.9/5  (35)
(35)
Find the coordinates of the point located four units in front of the -plane, nine units to the right of the -plane, and three units below the -plane.
(Multiple Choice)
4.7/5  (37)
(37)
Find the angle between the vectors and . Express your answer in degrees and round to the nearest tenth of a degree.
(Multiple Choice)
4.7/5  (39)
(39)
Find the general form of the equation of the plane with the given characteristics.
The plane passes through the point and is parallel to the -plane.
(Multiple Choice)
4.9/5  (33)
(33)
Find the general form of the equation of the plane passing through the three points. [Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.]
(Multiple Choice)
4.7/5  (36)
(36)
The weight of a crate is 200 newtons. Find the tension in each of the supporting cables shown in the figure. The coordinates of the points , and are given below the figure. Round to the nearest newton.
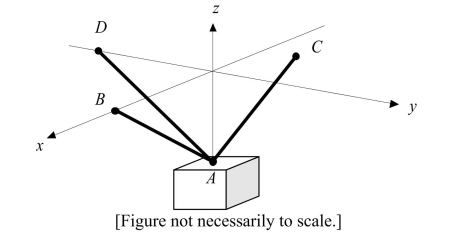 point , point , point , point
point , point , point , point
(Multiple Choice)
4.8/5  (37)
(37)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)