Exam 17: Introduction to Nonparametric Statistics

If we are interested in testing to determine whether the center of three or more populations is equal when the data in the samples are ordinal, what is the appropriate test to conduct?

A large sample Mann-Whitney U test should be used when the sample sizes exceed 20.

If a two-tailed Wilcoxon Matched-Pairs Signed Rank test is conducted for a sample of n = 8 and an alpha level equal to .05, the critical value is:

Assume that a Kruskal-Wallis test is being conducted to determine whether or not the medians of three populations are equal. The sum of rankings and the sample size for each group are below. 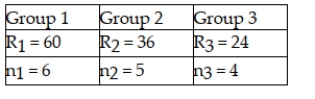The value of the test statistic is H = 0.68

A survey was recently conducted in which random samples of car owners of Chrysler, GM, and Ford cars were surveyed to determine their satisfaction. Each owner was asked to rate overall satisfaction on a scale of 1 (poor) to 1000 (excellent). The following data were recorded: 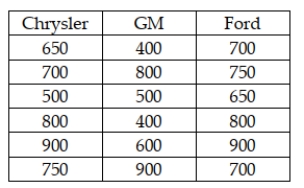If the analysts are not willing to assume that the population ratings are normally distributed and will use the Kruskal-Wallis test to determine if the three companies have different median ratings, what is correct test statistic for these data?

Recently, a study was done to determine whether the median speed on a section of highway is the same for cars versus trucks. A sample of 12 cars (n1 = 12) and 15 trucks (n2 = 15) was collected. If the Mann-Whitney U test is to be performed using an alpha = .05, the test critical U value is 49.

Recently, Major League Baseball officials stated that the median cost for a family of four to attend a baseball game including, parking, tickets, food, and drinks did not exceed $125.00. The following sample data were collected: 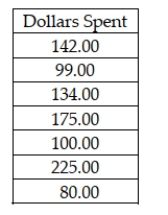Assuming that the test of the owners' claim is going to be conducted using an alpha = .05 level, the critical value is t = 1.9432.

Recently, a study was done to determine whether the median speed on a section of highway is the same for cars versus trucks. A sample of 12 cars (n1 = 12) and 15 trucks (n2 = 15) was collected. If the Mann-Whitney U test is to be performed using an alpha = .05 and if the U test statistic is calculated to be 68, the null hypothesis should be rejected.

A claim was recently made that stated that the median income for male and female graduates is the same for those graduating with a degree in operations management. The following sample data were collected: 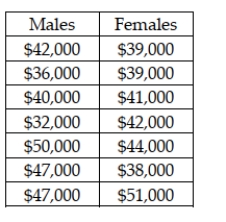In employing the Mann-Whitney U test, the U test statistic for the males is 43.5

The Wilcoxon signed rank test is used to test which of the following type of hypotheses?

The makers of furnace filters recently conducted a test to determine whether the median number of particulates that would pass through their four leading filters was the same. A random sample of 6 of each type of filter was used with the following data being recorded: 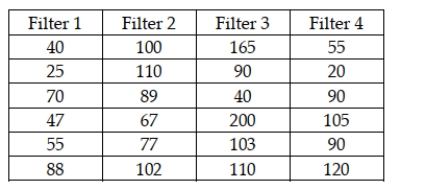If the Kruskal-Wallis test is used, the test statistic is approximately H = 7.814

The Wilcoxon signed rank test can be a one or two-tailed test similar to hypothesis tests for population means.

In using the Kruskal-Wallis test the sample sizes for each population must be equal.

The General Electric service department believes that the median time for a service call should be 30 or fewer minutes. To test this, the following random sample of service times was collected: 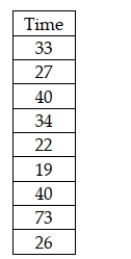Given that the managers do not wish to make the assumption that the population is normally distributed, the appropriate statistical test for testing about service times is:

The procedure of the Wilcoxon signed rank test is the same for either small or large sample sizes.

The Wilcoxon signed rank test is used to test hypotheses about the population median.

In order to determine whether the median distance for the X-Special golf ball exceeds the median distance for the best-selling golf ball, six golfers were selected and asked to hit each ball with their driver. The distance was recorded. The following data were observed. 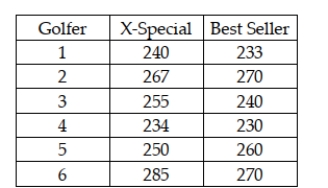Based on these, the appropriate test is the Kruskal-Wallis one-way analysis of variance.

Consider the situation in which a study was recently conducted to determine whether the median price of houses is the same in Seattle and Phoenix. The following data were collected. 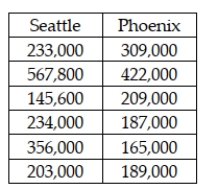Given these data, if a Mann-Whitney U test is to be used, the test statistic is:

The following null and alternative hypotheses are appropriate when using a Wilcoxon signed rank test. H0 : Population Median equals 14.5 HA : Population Median is not equal to 14.5

If a decision maker believes that the population is normally distributed and the data are known to be ratio level, then the either the t-test or the Wilcoxon signed rank test can be used to test null hypotheses about a single population mean.