Exam 13: Goodness-Of-Fit Tests and Contingency Analysis

Consider a goodness-of-fit test with a computed value of chi-square = 27.385 and a critical value = 13.388, the appropriate conclusion would be to:

What does the term expected cell frequencies refer to?

The goodness-of-fit test is essentially determining if the test statistic is significantly larger than zero.

In a chi-square contingency analysis, when expected cell frequencies drop below 5, the calculated chi- square value tends to be inflated and may inflate the true probability of ________ beyond the stated significance level.

A walk-in medical clinic believes that arrivals are uniformly distributed over weekdays (Monday through Friday). It has collected the following data based on a random sample of 100 days. 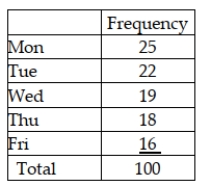Based on this information how many degrees for freedom are involved in this goodness of fit test?

The degrees of freedom for a contingency table with 15 rows and 11 columns is:

A lube and oil change business believes that the number of cars that arrive for service is the same each day of the week. If the business is open six days a week (Monday - Saturday) and a random sample of n = 200 customers is selected, the critical value for testing the hypothesis using a goodness-of-fit test is x2 = 9.2363 if the alpha level for the test is set at .10.

In a goodness-of-fit test, when the null hypothesis is true, the expected value for the chi-square test statistic is < zero.

A survey was recently conducted in which males and females were asked whether they owned a laptop personal computer. The following data were observed: 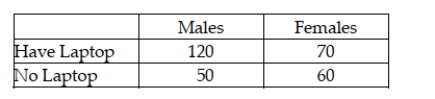Given this information, if having a laptop is independent of gender, the expected number of males with laptops in this survey is 150.

A study was recently conducted in which people were asked to indicate which news medium was their preferred choice for national news. The following data were observed: 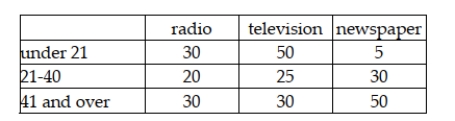Given this data, if we wish to test whether the preferred news source is independent of age with an alpha equal to .05, the critical value will be a chi-square value with 9 degrees of freedom.

A study was recently done in the United States in which car owners were asked to indicate whether their most recent car purchase was a U.S. car, a German car, or a Japanese car. The people in the survey were divided by geographic region in the United States. The following data were recorded. 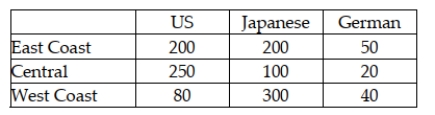Given this situation, to test whether the car origin is independent of the geographical location of the buyer, the expected number of people in the sample who bought a German made car and who lived on the East Coast is just under 40 people.

What does the term observed cell frequencies refer to?

A goodness-of-fit test can be used to determine whether a set of sample data comes from a specific hypothesized population distribution.

A study was recently done in the United States in which car owners were asked to indicate whether their most recent car purchase was a U.S. car, a German car, or a Japanese car. The people in the survey were divided by geographic region in the United States. The following data were recorded. 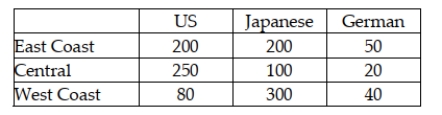Given this situation, to test whether the car origin is independent of the geographical location of the buyer, the sum of the expected cell frequencies will equal 1,240.

A walk-in medical clinic believes that arrivals are uniformly distributed over weekdays (Monday through Friday). It has collected the following data based on a random sample of 100 days. 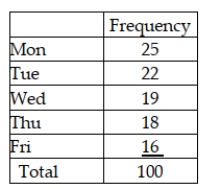Based on these data, conduct a goodness-of-fit test using a 0.10 level of significance. Which conclusion is correct?

Contingency analysis is used only for numerical data.

By combining cells we guard against having an inflated test statistic that could have led us to incorrectly reject the H0.

A cell phone company wants to determine if the use of text messaging is independent of age. The following data has been collected from a random sample of customers. 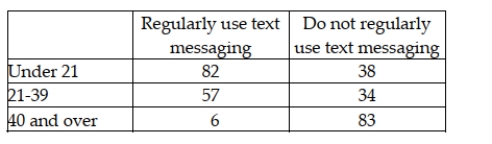To conduct a contingency analysis, the number of degrees of freedom is:

If one or more parameters are left unspecified in a goodness-of-fit test, they must be estimated from the sample data and one degree of freedom is lost for each parameter that must be estimated.

A business with 5 copy machines keeps track of how many copy machines need service on a given day. It believes this is binomially distributed with a probability of p = 0.2 of each machine needing service on any given day. It has collected the following based on a random sample of 100 days. 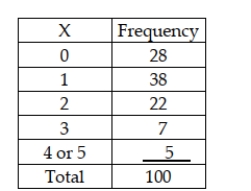Given this information, assuming that all expected values are sufficiently large to use the classes as shown above, the critical value based on a 0.05 level of significance is 9.4877.