Exam 7: Introduction to Sampling Distributions
Exam 1: The Where, Why, and How of Data Collection167 Questions
Exam 2: Graphs, Charts and Tablesdescribing Your Data138 Questions
Exam 3: Describing Data Using Numerical Measures138 Questions
Exam 4: Introduction to Probability125 Questions
Exam 5: Discrete Probability Distributions161 Questions
Exam 6: Introduction to Continuous Probability Distributions122 Questions
Exam 7: Introduction to Sampling Distributions136 Questions
Exam 8: Estimating Single Population Parameters174 Questions
Exam 9: Introduction to Hypothesis Testing183 Questions
Exam 10: Estimation and Hypothesis Testing for Two Population Parameters121 Questions
Exam 11: Hypothesis Tests and Estimation for Population Variances69 Questions
Exam 12: Analysis of Variance162 Questions
Exam 13: Goodness-Of-Fit Tests and Contingency Analysis105 Questions
Exam 14: Introduction to Linear Regression and Correlation Analysis139 Questions
Exam 15: Multiple Regression Analysis and Model Building148 Questions
Exam 16: Analyzing and Forecasting Time-Series Data131 Questions
Exam 17: Introduction to Nonparametric Statistics103 Questions
Exam 18: Introducing Business Analytics48 Questions
Exam 19: Introduction to Decision Analysis48 Questions
Exam 20: Introduction to Quality and Statistical Process Control42 Questions
Select questions type
The Dilmart Company has 8,000 parts in inventory. The mean dollar value of these parts is $10.79 with a standard deviation equal to $3.34. Suppose the inventory manager selected a random sample of n = 64 parts from the inventory and found a sample mean equal to $11.27. The probability of getting a sample mean at least as large as $11.27 is approximately 0.444.
Free
(True/False)
4.7/5  (35)
(35)
Correct Answer:
False
Suppose that a population is known to be normally distributed with mean = 2,000 and standard deviation = 230. If a random sample of size n = 8 is selected, calculate the probability that the sample mean will exceed 2,100.
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
D
A normally distributed population has a mean of 500 and a standard deviation of 60. Determine the probability that a random sample of size 25 selected from the population will have a sample mean greater than or equal to 515.
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
A random sample of 100 items is selected from a population of size 350. What is the probability that the sample mean will exceed 200 if the population mean is 195 and the population standard deviation equals 20? (Hint: Use the finite correction factor since the sample size is more than 5% of the population size.)
(Multiple Choice)
4.9/5  (42)
(42)
The State Department of Weights and Measures is responsible for making sure that commercial weighing and measuring devices, such as scales, are accurate so customers and businesses are not cheated. Periodically, employees of the department go to businesses and test their scales. For example, a dairy bottles milk in 1-gallon containers. Suppose that if the filling process is working correctly, the mean volume of all gallon containers is 1.00 gallon with a standard deviation equal to 0.10 gallon. Based on this information, if the department employee selects a random sample of n = 9 containers, what is the probability that the mean volume for the sample will be greater than 1.01 gallons?
(Multiple Choice)
4.8/5  (34)
(34)
The State Department of Weights and Measures is responsible for making sure that commercial weighing and measuring devices, such as scales, are accurate so customers and businesses are not cheated. Periodically, employees of the department go to businesses and test their scales. For example, a dairy bottles milk in 1-gallon containers. Suppose that if the filling process is working correctly, the mean volume of all gallon containers is 1.00 gallon with a standard deviation equal to 0.10 gallon. The department's test process requires that they select a random sample of n = 9 containers. If the sample mean is less than 0.97 gallon, the department will fine the dairy. Based on this information, suppose that the dairy wants no more than a 0.05 chance of being fined, which of the following options exist if they can't alter the filling standard deviation?
(Multiple Choice)
4.8/5  (35)
(35)
Which of the following statements is true with respect to the sampling distribution of a proportion?
(Multiple Choice)
5.0/5  (36)
(36)
One of the nation's biggest regional airlines has tracked 4,000 landings and take-offs during the past month. Treating these data as the population of interest, the company found that the average time the planes spent on the ground (called the turn time) was 17.23 minutes with a standard deviation of 3.79 minutes. Further, they determined that the distribution of turn times is normally distributed. Then, the probability that a single turn time selected at random from this population would exceed 20 minutes is approximately 0.2327.
(True/False)
5.0/5  (41)
(41)
If it is desired that sampling error be reduced, one step that tends to work is to increase the sample size that is selected from the population.
(True/False)
4.9/5  (31)
(31)
A major shipping company has stated that 96 percent of all parcels are delivered on time. To check this, a random sample of n = 200 parcels were sampled. Of these, 184 arrived on time. If the company's claim is correct, what is the probability of 184 or fewer parcels arriving on time?
(Multiple Choice)
4.7/5  (31)
(31)
A particular subdivision has 20 homes. The number of people living in each of these homes is listed as follows: 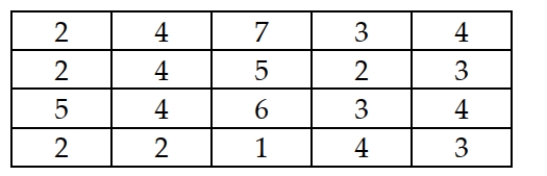 Which of the following statements is true when comparing a random sample of size three homes selected from the population to a random sample of size 6 homes selected from the population?
Which of the following statements is true when comparing a random sample of size three homes selected from the population to a random sample of size 6 homes selected from the population?
(Multiple Choice)
4.9/5  (26)
(26)
The size of the standard error of the sample proportion is dependent on the value of the population proportion and the closer the population proportion is to .50, the larger the standard error for a given sample size will be.
(True/False)
4.9/5  (43)
(43)
A population has a proportion equal to 0.30. Calculate the following probabilities with n = 100. Find
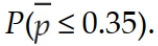
(Multiple Choice)
4.9/5  (30)
(30)
A population has a proportion equal to 0.30. Calculate the following probabilities with n = 100. Find P( ≥ 0.27).
(Multiple Choice)
4.8/5  (36)
(36)
Given a population in which the probability of success is p = 0.20, if a sample of 500 items is taken, then calculate the probability the proportion of successes in the sample will be between 0.18 and 0.23 if the sample size is 200.
(Multiple Choice)
4.8/5  (35)
(35)
A population, with an unknown distribution, has a mean of 80 and a standard deviation of 7. For a sample of 49, the probability that the sample mean will be larger than 82 is:
(Multiple Choice)
5.0/5  (37)
(37)
According to the most recent Labor Department data, 10.5% of engineers (electrical, mechanical, civil, and industrial) were women. Suppose a random sample of 50 engineers is selected. How likely is it that the random sample will contain fewer than 5 women in these positions?
(Multiple Choice)
4.8/5  (35)
(35)
Regardless of the value of the population proportion, p, (with the obvious exceptions of p = 0 and p =1) the sampling distribution for the sample proportion, will be approximately normally distributed providing that the sample size is large enough.
(True/False)
4.8/5  (27)
(27)
A sampling distribution is the distribution of the individual values that are included in a sample from a population.
(True/False)
4.9/5  (38)
(38)
A normally distributed population has a mean of 500 and a standard deviation of 60. Determine the probability that a random sample of size 16 selected from this population will have a sample mean less than 475.
(Multiple Choice)
4.8/5  (38)
(38)
Showing 1 - 20 of 136
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)