Exam 3: A: Algorithms
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
Prove that
Free
(Short Answer)
5.0/5  (43)
(43)
Correct Answer:
is since (if . Also, is ) since (if ).
assume that the number of multiplications of entries used to multiply a p × q and a q × r matrix is pqr.
-What is the best order to form the product ABC if A, B and C are matrices with dimensions 2 × 5, 5 × 7 and 7 × 3, respectively?
Free
(Essay)
4.9/5  (33)
(33)
Correct Answer:
(AB)C uses 2 · 5 · 7 + 2 · 7 · 3 = 112 multiplications, fewer than A(BC), which uses 5 · 7 · 3 + 2 · 5 · 3 = 135.
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-The worst-case analysis of a linear search of a list of size n (counting the number of comparisons)
Free
(Short Answer)
4.7/5  (44)
(44)
Correct Answer:
n
find the best big-O function for the function. Choose your answer from among the following:
-
(Short Answer)
4.8/5  (29)
(29)
Describe an algorithm that takes a list of n integers a1, a2, . . . , an and finds the number of integers each greater than five in the list.
(Short Answer)
4.8/5  (36)
(36)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-The number of print statements in the following:
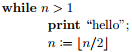
(Short Answer)
4.8/5  (33)
(33)
List all the steps that the naive string matcher uses to match the pattern xy in the text yxyxxy.
(Essay)
4.9/5  (40)
(40)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-An iterative algorithm to compute n!, (counting the number of multiplications)
(Short Answer)
4.7/5  (29)
(29)
Suppose you have two different algorithms for solving a problem. To solve a problem of size n, the first algorithm uses exactly operations and the second algorithm uses exactly operations. As n grows, which algorithm uses fewer operations?
(Essay)
4.9/5  (36)
(36)
List all the steps the binary search algorithm uses to search for 27 in the following list: 5, 6, 8, 12, 15, 21, 25, 31.
(Essay)
4.9/5  (33)
(33)
Describe an algorithm that takes a list of n integers and finds the average of the largest and smallest
(Essay)
4.9/5  (30)
(30)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-An algorithm that finds the average of n numbers by adding them and dividing by n
(Short Answer)
4.9/5  (33)
(33)
assume that the number of multiplications of entries used to multiply a p × q and a q × r matrix is pqr.
-What is the most efficient way to multiply the matrices A1, A2, A3 of sizes 10 × 50, 50 × 10, 10 × 40?
(Short Answer)
4.9/5  (29)
(29)
Give a big-O estimate for the number of operations (where an operation is an addition or a multiplication) used in this segment of an algorithm:
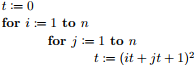
(Short Answer)
4.9/5  (31)
(31)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-An algorithm that prints all bit strings of length n.
(Short Answer)
4.9/5  (35)
(35)
Arrange the functions in a list so that each function is big-O of the next function.
(Short Answer)
4.8/5  (46)
(46)
Showing 1 - 20 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)