Exam 13: A: Modeling Computation
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
Suppose a phrase-structure grammar has productions S → S11, S → 0A, S → A1, A → 0. Find a derivation of 01.
Free
(Short Answer)
4.8/5  (41)
(41)
Correct Answer:
Find a grammar for the set
Free
(Essay)
4.9/5  (36)
(36)
Correct Answer:
Use the grammar with productions and , where S is the start symbol.
Suppose a phrase-structure grammar has productions S → 1S0, S → 0A, A → 0. Find a derivation of 00.
(Short Answer)
4.8/5  (37)
(37)
Construct a finite-state automaton that recognizes all strings that end with 11.
(Essay)
4.9/5  (36)
(36)
What language is generated by the phrase-structure grammar if the productions are where is the start symbol?
(Essay)
4.9/5  (30)
(30)
Suppose a phrase-structure grammar has productions S → S11, S → 0A, S → A1, A → 0. Find a derivation of 0011.
(Short Answer)
4.9/5  (39)
(39)
For the following Turing machines T , find the final tape when T is run on the following tape, beginning in the initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots ,0,,0,R , ,1,,0,R , ,0,,1,R , ,1,,1,L , ,B,,1,L
(Short Answer)
4.9/5  (44)
(44)
let resulting grammar G is (i) type 0 grammar, but not type 1 ,
(ii) type 1 grammar, but not type 2 ,
(iii) type 2 grammar, but not type 3 ,
(iv) type 3 grammar.
-
(Short Answer)
4.8/5  (30)
(30)
Find a production of the form "A → ____" such that S → 1S , S → 0A, A → ____ produces {1n00 | n ≥ 0}.
(Short Answer)
4.8/5  (33)
(33)
Suppose a phrase-structure grammar has productions S → 1S0, S → 0A, A → 0. Find a derivation of
(Short Answer)
4.9/5  (33)
(33)
For the following Turing machine T , find the final tape when T is run on the following tape, beginning in the initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots ,0,,0,R , ,B,,1,R , ,0,,1,R , ,0,,1,L , ,1,,1,R
(Short Answer)
4.8/5  (33)
(33)
Find the set recognized by this deterministic finite-state machine. 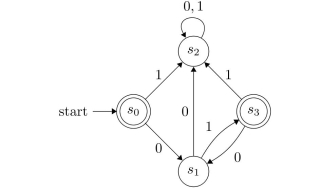
(Short Answer)
4.9/5  (33)
(33)
What is the language generated by the grammar with productions , and , where S is the start symbol?
(Essay)
4.8/5  (27)
(27)
Which strings belong to the regular set represented by the regular expression (1∗01∗0) ?
(Short Answer)
4.8/5  (28)
(28)
Showing 1 - 20 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)