Exam 13: A: Modeling Computation
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
Let G be the phrase-structure grammar with vocabulary V={A, B, a, b, S} , terminal element set T={a, b} , start symbol S , and production set P=
are derivable from S ?
(1) ba ,
(2) ab ,
(3) baab,
(4) aababa,
(5) aba
(Short Answer)
4.8/5  (35)
(35)
Construct a finite-state machine with output that produces a 1 if and only if the last 3 input bits read are 0's.
(Essay)
4.8/5  (34)
(34)
let resulting grammar G is (i) type 0 grammar, but not type 1 ,
(ii) type 1 grammar, but not type 2 ,
(iii) type 2 grammar, but not type 3 ,
(iv) type 3 grammar.
-
(Short Answer)
4.8/5  (35)
(35)
For the following Turing machine T , find the final tape when T is run on the following tape, beginning in the initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots ,0,,1,R , ,1,,0,R , ,1,,1,R , ,B,,0,R .
(Short Answer)
5.0/5  (31)
(31)
Suppose a phrase-structure grammar has productions S → S11, S → 0A, S → A1, A → 0. Find a derivation of 011111.
(Short Answer)
4.7/5  (40)
(40)
Suppose a phrase-structure grammar has productions S → S0, S → A1, A → 0. Find a derivation of 0100.
(Short Answer)
4.9/5  (30)
(30)
let resulting grammar G is (i) type 0 grammar, but not type 1 ,
(ii) type 1 grammar, but not type 2 ,
(iii) type 2 grammar, but not type 3 ,
(iv) type 3 grammar.
-
(Short Answer)
4.9/5  (35)
(35)
What is the output produced by this finite-state machine when the input string is 11101? 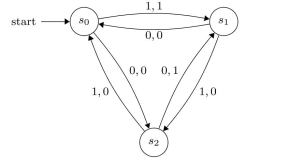
(Short Answer)
4.8/5  (38)
(38)
Suppose that A = {1, 11, 01} and B = {0, 10}. Find BA. this state table.
(Short Answer)
4.7/5  (29)
(29)
let resulting grammar G is (i) type 0 grammar, but not type 1 ,
(ii) type 1 grammar, but not type 2 ,
(iii) type 2 grammar, but not type 3 ,
(iv) type 3 grammar.
-
(Short Answer)
4.8/5  (41)
(41)
Which strings are recognized by the following finite-state automaton? 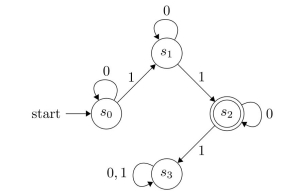
(Short Answer)
4.7/5  (31)
(31)
For the following Turing machine T , find the final tape when T is run on the following tape, beginning in the initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots ,0,,1,R , ,1,,1,L , ,0,,1,L
(Short Answer)
4.9/5  (32)
(32)
let resulting grammar G is (i) type 0 grammar, but not type 1 ,
(ii) type 1 grammar, but not type 2 ,
(iii) type 2 grammar, but not type 3 ,
(iv) type 3 grammar.
-
(Short Answer)
4.7/5  (39)
(39)
Suppose V={S, A, a, b}, T={a, b} , and S is the start symbol. Find a set of productions that includes and and generates the language {a, a a} .
(Short Answer)
4.8/5  (34)
(34)
Suppose a phrase-structure grammar has productions S → S0, S → A1, A → 0. Find a derivation of 010.
(Short Answer)
4.7/5  (40)
(40)
Showing 41 - 60 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)