Exam 14: Introduction to Multiple Regression
Exam 1: Introduction145 Questions
Exam 2: Organizing and Visualizing Data210 Questions
Exam 3: Numerical Descriptive Measures153 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions218 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions191 Questions
Exam 7: Sampling and Sampling Distributions197 Questions
Exam 8: Confidence Interval Estimation196 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests165 Questions
Exam 10: Two-Sample Tests210 Questions
Exam 11: Analysis of Variance213 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests201 Questions
Exam 13: Simple Linear Regression213 Questions
Exam 14: Introduction to Multiple Regression355 Questions
Exam 15: Multiple Regression Model Building96 Questions
Exam 16: Time-Series Forecasting168 Questions
Exam 17: Statistical Applications in Quality Management133 Questions
Exam 18: A Roadmap for Analyzing Data54 Questions
Exam 19: Questions that Involve Online Topics321 Questions
Select questions type
TABLE 14-19
The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0) and 15 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Atitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age).
The Minitab output is given below: 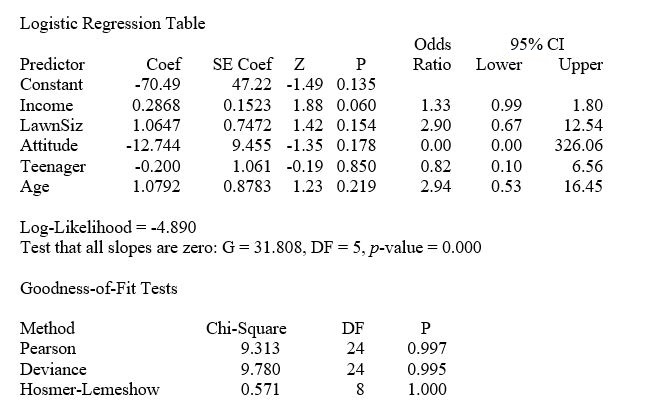 -Referring to Table 14-19, which of the following is the correct interpretation for the Attitude slope coefficient?
-Referring to Table 14-19, which of the following is the correct interpretation for the Attitude slope coefficient?
(Multiple Choice)
4.8/5  (42)
(42)
TABLE 14-10
You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual, the number of traffic tickets received by the individual, and the population density of the city in which the individual lives. You performed a regression analysis in Excel and obtained the following information:
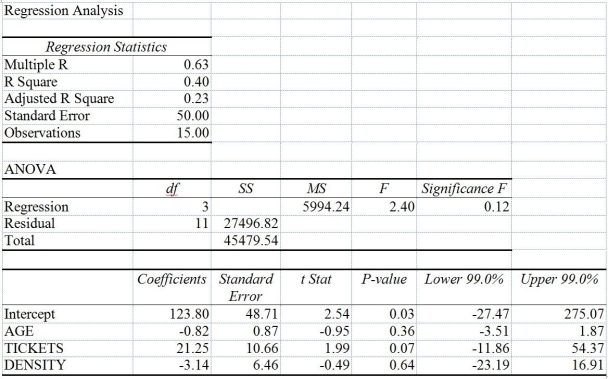 -Referring to Table 14-10, the standard error of the estimate is ________.
-Referring to Table 14-10, the standard error of the estimate is ________.
(Short Answer)
4.8/5  (38)
(38)
TABLE 14-17

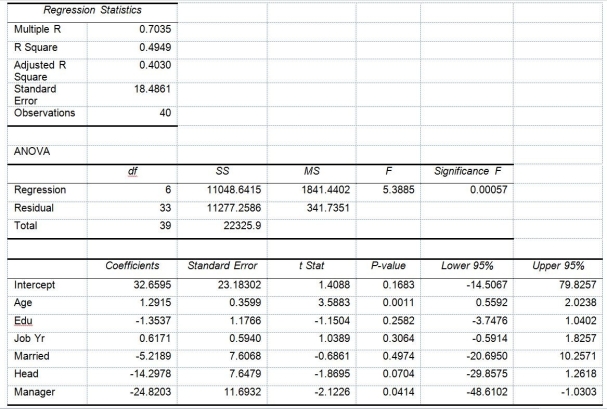 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
 -Referring to Table 14-17 Model 1, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
-Referring to Table 14-17 Model 1, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
(Multiple Choice)
5.0/5  (36)
(36)
TABLE 14-17

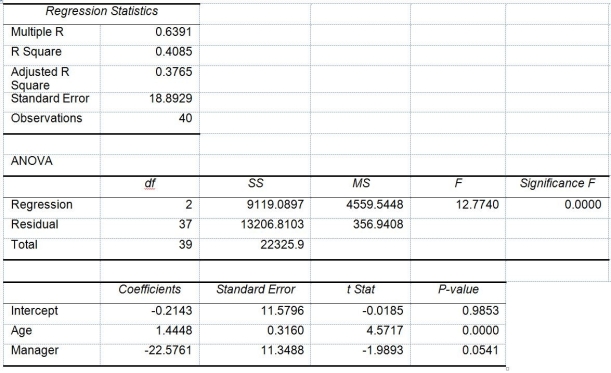
 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
 -Referring to Table 14-17 Model 1, what is the value of the test statistic when testing whether being married or not makes a difference in the mean number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
-Referring to Table 14-17 Model 1, what is the value of the test statistic when testing whether being married or not makes a difference in the mean number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
(Short Answer)
4.9/5  (36)
(36)
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below: 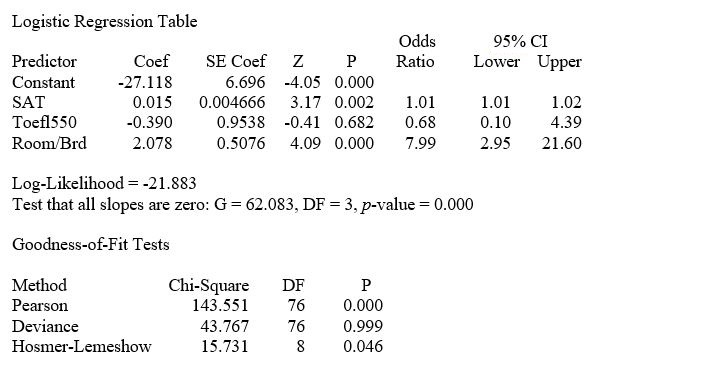 -Referring to Table 14-18, there is not enough evidence to conclude that the model is not a good-fitting model at a 0.05 level of significance.
-Referring to Table 14-18, there is not enough evidence to conclude that the model is not a good-fitting model at a 0.05 level of significance.
(True/False)
4.9/5  (33)
(33)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
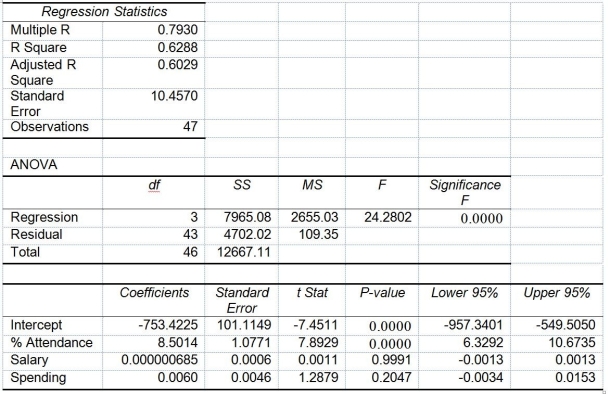 -Referring to Table 14-15, the null hypothesis should be rejected at a 5% level of significance when testing whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables.
-Referring to Table 14-15, the null hypothesis should be rejected at a 5% level of significance when testing whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables.
(True/False)
4.8/5  (36)
(36)
TABLE 14-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. 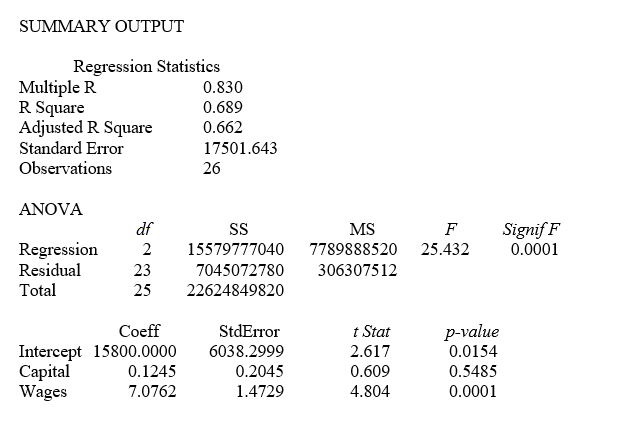 -Referring to Table 14-5, what is the p-value for Wages?
-Referring to Table 14-5, what is the p-value for Wages?
(Multiple Choice)
4.8/5  (32)
(32)
TABLE 14-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following 4 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X₁) the amount of insulation in inches (X₂), the number of windows in the house (X₃), and the age of the furnace in years (X₄). Given below are the Excel outputs of two regression models.
Model 1
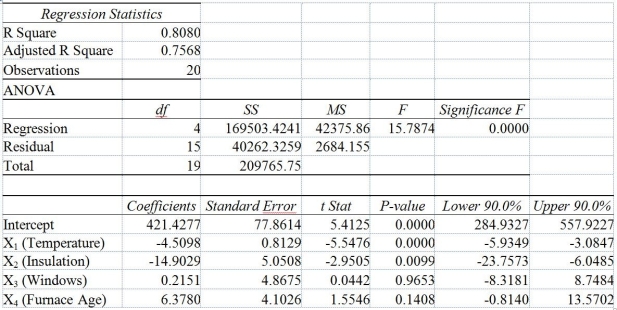 Model 2
Model 2
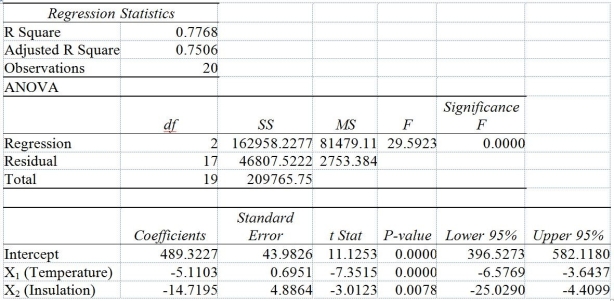 -Referring to Table 14-6, what is your decision and conclusion for the test H₀: β₂ = 0 vs H₁: β₂ < 0 at the α = 0.01 level of significance using Model 1?
-Referring to Table 14-6, what is your decision and conclusion for the test H₀: β₂ = 0 vs H₁: β₂ < 0 at the α = 0.01 level of significance using Model 1?
(Multiple Choice)
4.9/5  (31)
(31)
TABLE 14-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size), and education of the head of household (School). House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: 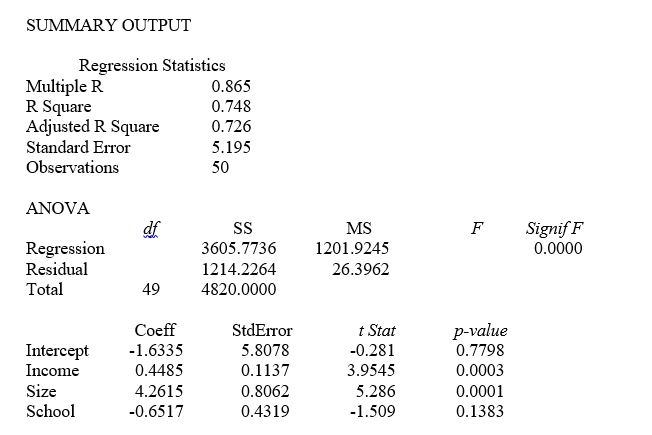 -Referring to Table 14-4, what is the predicted house size (in hundreds of square feet) for an individual earning an annual income of $40,000, having a family size of 4, and going to school a total of 13 years?
-Referring to Table 14-4, what is the predicted house size (in hundreds of square feet) for an individual earning an annual income of $40,000, having a family size of 4, and going to school a total of 13 years?
(Multiple Choice)
4.7/5  (43)
(43)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
 -Referring to Table 14-15, what is the standard error of estimate?
-Referring to Table 14-15, what is the standard error of estimate?
(Short Answer)
4.8/5  (34)
(34)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
 -Referring to Table 14-15, what are the lower and upper limits of the 95% confidence interval estimate for the effect of a one dollar increase in instructional spending per pupil on the mean percentage of students passing the proficiency test?
-Referring to Table 14-15, what are the lower and upper limits of the 95% confidence interval estimate for the effect of a one dollar increase in instructional spending per pupil on the mean percentage of students passing the proficiency test?
(Short Answer)
4.8/5  (33)
(33)
When an explanatory variable is dropped from a multiple regression model, the adjusted r² can increase.
(True/False)
4.7/5  (28)
(28)
TABLE 14-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X₁) and the number of economics courses the employee successfully completed in college (X₂). The professor randomly selects 6 workers and collects the following information: 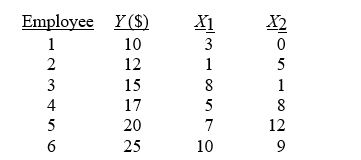 -Referring to Table 14-2, suppose an employee had never taken an economics course and managed to score a 5 on his performance rating. What is his estimated expected wage rate?
-Referring to Table 14-2, suppose an employee had never taken an economics course and managed to score a 5 on his performance rating. What is his estimated expected wage rate?
(Multiple Choice)
4.7/5  (35)
(35)
TABLE 14-17

 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
 -Referring to Table 14-17 Model 1, there is sufficient evidence that all of the explanatory variables are related to the number of weeks a worker is unemployed due to a layoff at a 10% level of significance.
-Referring to Table 14-17 Model 1, there is sufficient evidence that all of the explanatory variables are related to the number of weeks a worker is unemployed due to a layoff at a 10% level of significance.
(True/False)
4.8/5  (35)
(35)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
 -Referring to Table 14-15, you can conclude that instructional spending per pupil has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 5% level of significance using the 95% confidence interval estimate for β₃.
-Referring to Table 14-15, you can conclude that instructional spending per pupil has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 5% level of significance using the 95% confidence interval estimate for β₃.
(True/False)
4.9/5  (40)
(40)
TABLE 14-10
You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual, the number of traffic tickets received by the individual, and the population density of the city in which the individual lives. You performed a regression analysis in Excel and obtained the following information:
 -Referring to Table 14-10, the adjusted r² is ________.
-Referring to Table 14-10, the adjusted r² is ________.
(Short Answer)
4.8/5  (33)
(33)
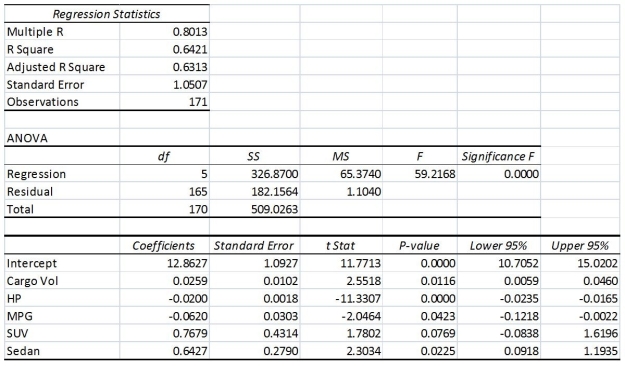
TABLE 14-16
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 The various residual plots are as shown below.
The various residual plots are as shown below.
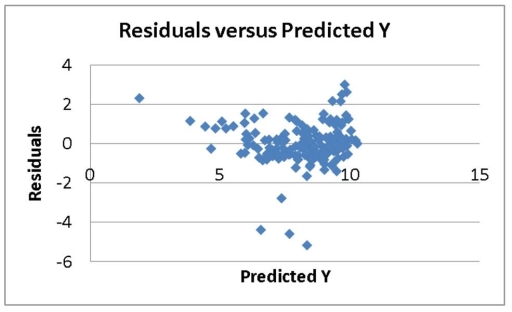
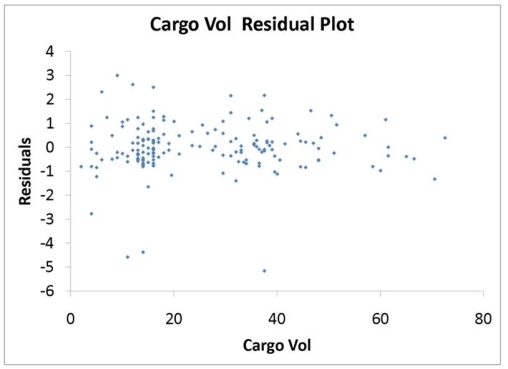
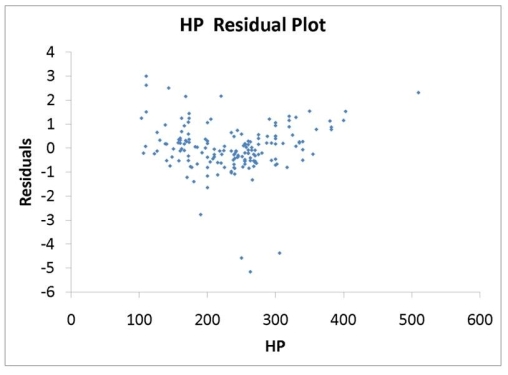
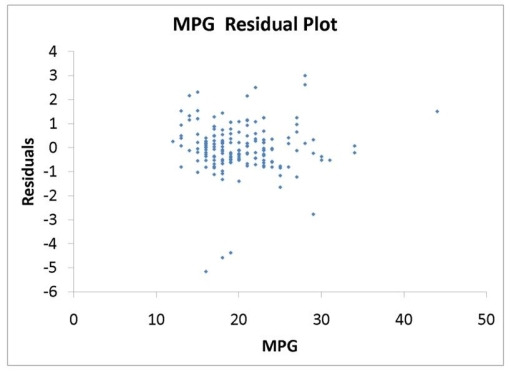
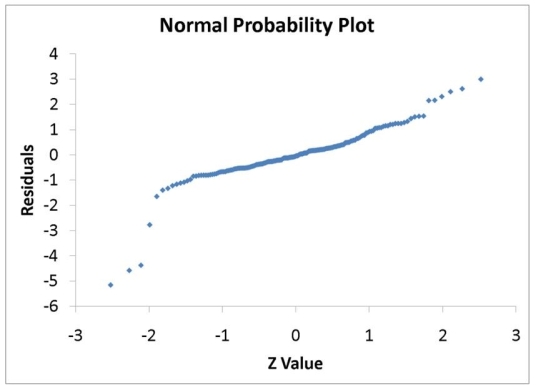
 -Referring to 14-16, which of the following assumptions is most likely violated based on the residual plot for HP?
-Referring to 14-16, which of the following assumptions is most likely violated based on the residual plot for HP?
(Multiple Choice)
4.9/5  (35)
(35)
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below:  -Referring to Table 14-18, which of the following is the correct interpretation for the SAT slope coefficient?
-Referring to Table 14-18, which of the following is the correct interpretation for the SAT slope coefficient?
(Multiple Choice)
4.8/5  (34)
(34)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
 -Referring to Table 14-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
-Referring to Table 14-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
(Multiple Choice)
4.8/5  (36)
(36)
Showing 241 - 260 of 355
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)