Exam 43: Molecules and Solids
Exam 1: Physics and Measurement25 Questions
Exam 2: Motion in One Dimension66 Questions
Exam 3: Vectors47 Questions
Exam 4: Motion in Two Dimensions79 Questions
Exam 5: The Laws of Motion113 Questions
Exam 6: Circular Motion and Other Applications of Newtons Laws55 Questions
Exam 7: Energy of a System74 Questions
Exam 8: Conservation of Energy84 Questions
Exam 9: Linear Momentum and Collisions89 Questions
Exam 10: Rotation of a Rigid Object About a Fixed Axis82 Questions
Exam 11: Angular Momentum46 Questions
Exam 12: Static Equilibrium and Elasticity34 Questions
Exam 13: Universal Gravitation47 Questions
Exam 14: Fluid Mechanics53 Questions
Exam 15: Oscillatory Motion41 Questions
Exam 16: Wave Motion82 Questions
Exam 18: Superposition and Standing Waves72 Questions
Exam 19: Temperature47 Questions
Exam 20: The First Law of Thermodynamics61 Questions
Exam 21: The Kinetic Theory of Gases38 Questions
Exam 22: Heat Engines, Entropy, and the Second Law of Thermodynamics55 Questions
Exam 23: Electric Fields67 Questions
Exam 24: Gausss Law82 Questions
Exam 25: Electric Potential111 Questions
Exam 26: Capacitance and Dielectrics63 Questions
Exam 27: Current and Resistance34 Questions
Exam 28: Direct-Current Circuits84 Questions
Exam 29: Magnetic Fields80 Questions
Exam 30: Sources of the Magnetic Field95 Questions
Exam 31: Faradays Law62 Questions
Exam 32: Inductance23 Questions
Exam 33: Alternating-Current Circuits65 Questions
Exam 34: Electromagnetic Waves40 Questions
Exam 35: The Nature of Light and the Principles of Ray Optics37 Questions
Exam 36: Image Formation43 Questions
Exam 37: Wave Optics48 Questions
Exam 38: Diffraction Patterns and Polarization47 Questions
Exam 39: Relativity34 Questions
Exam 40: Introduction to Quantum Physics48 Questions
Exam 41: Quantum Mechanics33 Questions
Exam 42: Atomic Physics59 Questions
Exam 43: Molecules and Solids46 Questions
Exam 44: Nuclear Structure89 Questions
Exam 46: Particle Physics and Cosmology34 Questions
Select questions type
Assume a diatomic molecule can be considered to be two point masses separated by a distance r. The center of mass of the system is located a distance x from m1, equal to
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
B
The energy gap for a semiconductor is 1.25 eV. Of the frequencies given below, what is the minimum frequency photon than can move an electron from the valence band to the conduction band?
Free
(Multiple Choice)
5.0/5  (38)
(38)
Correct Answer:
B
The energy gap for germanium is 0.670 eV at room temperature. What wavelength must a photon have (in nm) to excite the electron to the conduction band?
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
C
What is the energy of the first rotational state of the hydrogen (H2) molecule? The separation between the protons is 10−10 m and the mass of each proton is 1.67 × 10−27 kg. (h = 6.626 × 10−34 J ⋅ s and 1 eV = 1.6 × 10−19 J.)
(Short Answer)
4.8/5  (28)
(28)
An experiment determines that there are 49 allowed rotational energies for a diatomic molecule whose moment of inertia is 2 × 10−46 kg ⋅ m2. The maximum rotational kinetic energy (in eV) is
(Multiple Choice)
4.8/5  (35)
(35)
The rotational kinetic energy of a diatomic molecule can take the form
(Multiple Choice)
4.7/5  (28)
(28)
A diatomic molecule consists of two point masses, m1 and m2, separated by a distance r. If x is the distance from m1 to the center of mass, find the moment of inertia in terms of x about an axis perpendicular to the molecular axis through the center of mass.
(Multiple Choice)
4.9/5  (42)
(42)
The rotation spectrum of the HCl molecule suggests a photon in the far infrared (around 5.0 × 10−6 m) can excite the first rotational level. From this data, the moment of inertia of the HCl molecule (in kg ⋅ m2) is
(Multiple Choice)
4.8/5  (35)
(35)
The moment of inertia of a CO molecule is 1.46 × 10−46 kg ⋅ m2. What is the wavelength of the photon emitted if a rotational transition occurs from the J = 3 to the J = 2 state?
(Multiple Choice)
4.8/5  (32)
(32)
Assume the angular momentum of a diatomic molecule is quantized according to the relation 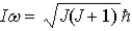 . What are the allowed rotational kinetic energies?
. What are the allowed rotational kinetic energies?
(Multiple Choice)
4.9/5  (34)
(34)
In the hydrogen molecule, H2, the separation between the protons is 10−10 m. If the molecule is in its first rotational energy state, what is the angular velocity of the molecule about its center of mass?
(Short Answer)
4.8/5  (34)
(34)
A diatomic molecule consists of two point masses, m1 and m2, separated by a distance r. Find the moment of inertia through the center of mass about an axis perpendicular to the molecular axis.
(Multiple Choice)
4.9/5  (30)
(30)
The force constant of HCl is 480 N/m. If the atomic masses are 1 u and 35 u (1 u = 1.66 × 10−27 kg), find the fundamental frequency (in Hz).
(Multiple Choice)
4.8/5  (34)
(34)
A molecule makes a transition from the J = 1 to the J = 0 rotational energy state. The wavelength of the emitted photon is 2.6 × 10−3 m. What is the moment of inertia of the molecule (in kg ⋅ m2)?
(Multiple Choice)
4.9/5  (32)
(32)
When calculating the rotational kinetic energy of a diatomic molecule, with atoms of mass m1 and m2,the moment of inertia about an axis passing through the molecule's center of mass, with r the atomic separation, is
(Multiple Choice)
4.8/5  (46)
(46)
When a molecule jumps from a rotational energy level characterized by the rotational quantum number J to one characterized by J − 1, the difference in energy of levels J and J − 1, EJ − EJ − 1, is
(Multiple Choice)
4.9/5  (38)
(38)
A diatomic molecule consists of two point masses, m1 and m2, separated by a distance r. If x is the distance from m1 to the center of mass, find the moment of inertia in terms of x about an axis parallel to the molecular axis through the center of mass.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 1 - 20 of 46
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)