Exam 14: Introduction to Multiple Regression

TABLE 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2 Yj. (Allvariables except $j$ ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201. Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations $\text { ANOVA }$ df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40 $\text { ANOVA }$ df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Table 14-17 Model 1, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?

TABLE 14-16 What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected: Accel Time: Acceleration time in sec. Cargo Vol: Cargo volume in cu. ft. HP: Horsepower MPG: Miles per gallon SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0 Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0 The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below. Regression Statistics Multiple R 0.8013 R Square 0.6421 Adjusted R Square 0.6313 Standard Error 1.0507 Observations 171 $\text { ANOVA }$ df SS MS F Significance F Regression 5 326.8700 65.3740 59.2168 0.0000 Residual 165 182.1564 1.1040 Total 170 509.0263 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 12.8627 1.0927 11.7713 0.0000 10.7052 15.0202 Cargo Vol 0.0259 0.0102 2.5518 0.0116 0.0059 0.0460 HP -0.0200 0.0018 -11.3307 0.0000 -0.0235 -0.0165 MPG -0.0620 0.0303 -2.0464 0.0423 -0.1218 -0.0022 SUV 0.7679 0.4314 1.7802 0.0769 -0.0838 1.6196 Sedan 0.6427 0.2790 2.3034 0.0225 0.0918 1.1935 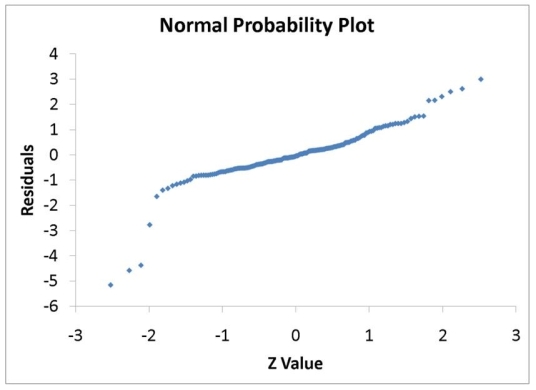The various residual plots are as shown below. 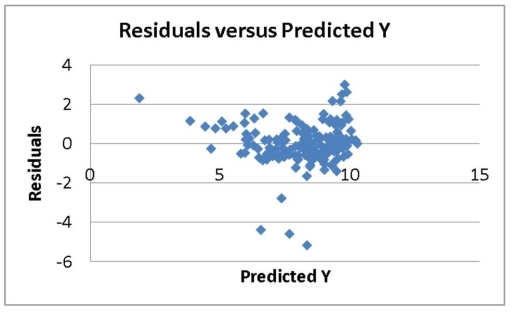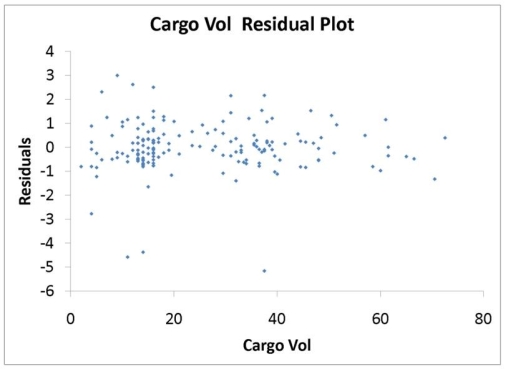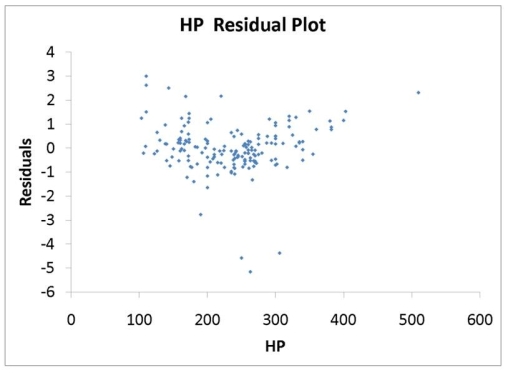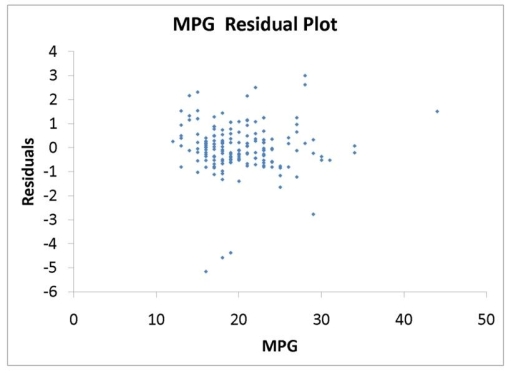The coefficients of partial determination $\left( R ^ { 2 }_{Y j} \right.$ . (All variables except $\left. j \right)$ of each of the 5 predictors are, respectively, $0.0380,0.4376,0.0248,0.0188$ , and $0.0312$ . The coefficient of multiple determination for the regression model using each of the 5 variables $X _ { j }$ as the dependent variable and all other $X$ variables as independent variables $\left( R _ { j } ^ { 2 } \right)$ are, respectively, $0.7461,0.5676,0.6764,0.8582,0.6632$ . -Referring to 14-16, ________ of the variation in Accel Time can be explained by the five independent variables.

TABLE 14-7 The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units (credits) and total SAT scores of each. She takes a sample of students and generates the following Microsoft Excel output: SUMMARY OUTPUT SUMMARY OUTPUT Regression Statistics Multiple R 0.916 R Square 0.839 Adjusted R Square 0.732 Standard Error 0.24685 Observations 6 ANOVA df SS MS F Signif F Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat p -value Intercept 4.593897 1.13374542 4.052 0.0271 Units -0.247270 0.06268485 -3.945 0.0290 SAT Total 0.001443 0.00101241 1.425 0.2494 -Referring to Table 14-7, the department head wants to test H₀: β₁ = β₂ = 0. The critical value of the F test for a level of significance of 0.05 is ________.

TABLE 14-19 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0) and 15 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Atitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age). The Minitab output is given below: Logistic Regression Table Odds 95\% CI Predictor Coef SE Coef Z P Ratio Lower Upper Constant -70.49 47.22 -1.49 0.135 Income 0.2868 0.1523 1.88 0.060 1.33 0.99 1.80 LawnSiz 1.0647 0.7472 1.42 0.154 2.90 0.67 12.54 Attitude -12.744 9.455 -1.35 0.178 0.00 0.00 326.06 Teenager -0.200 1.061 -0.19 0.850 0.82 0.10 6.56 Age 1.0792 0.8783 1.23 0.219 2.94 0.53 16.45 Log-Likelihood $= - 4.890$ Test that all slopes are zero: $\mathrm { G } = 31.808 , \mathrm { DF } = 5 , p$ -value $= 0.000$ Goodness-of-Fit Tests Method Chi-Square DF Pearson 9.313 24 0.997 Deviance 9.780 24 0.995 Hosmer-Lemeshow 0.571 8 1.000 -Referring to Table 14-19, what is the estimated probability that a 48-year-old home owner with a family income of $100,000, a lawn size of 5,000 square feet, a positive attitude toward outdoor recreation, and two teenagers in the household will purchase a lawn service?

TABLE 14-16 What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected: Accel Time: Acceleration time in sec. Cargo Vol: Cargo volume in cu. ft. HP: Horsepower MPG: Miles per gallon SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0 Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0 The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below. Regression Statistics Multiple R 0.8013 R Square 0.6421 Adjusted R Square 0.6313 Standard Error 1.0507 Observations 171 $\text { ANOVA }$ df SS MS F Significance F Regression 5 326.8700 65.3740 59.2168 0.0000 Residual 165 182.1564 1.1040 Total 170 509.0263 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 12.8627 1.0927 11.7713 0.0000 10.7052 15.0202 Cargo Vol 0.0259 0.0102 2.5518 0.0116 0.0059 0.0460 HP -0.0200 0.0018 -11.3307 0.0000 -0.0235 -0.0165 MPG -0.0620 0.0303 -2.0464 0.0423 -0.1218 -0.0022 SUV 0.7679 0.4314 1.7802 0.0769 -0.0838 1.6196 Sedan 0.6427 0.2790 2.3034 0.0225 0.0918 1.1935 The various residual plots are as shown below. The coefficients of partial determination $\left( R ^ { 2 }_{Y j} \right.$ . (All variables except $\left. j \right)$ of each of the 5 predictors are, respectively, $0.0380,0.4376,0.0248,0.0188$ , and $0.0312$ . The coefficient of multiple determination for the regression model using each of the 5 variables $X _ { j }$ as the dependent variable and all other $X$ variables as independent variables $\left( R _ { j } ^ { 2 } \right)$ are, respectively, $0.7461,0.5676,0.6764,0.8582,0.6632$ . -Referring to 14-16, the 0 to 60 miles per hour acceleration time of an SUV is predicted to be 0.1252 seconds higher than that of a sedan.

TABLE 14-10 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual, the number of traffic tickets received by the individual, and the population density of the city in which the individual lives. You performed a regression analysis in Excel and obtained the following information: $\text { Regression Analysis }$ Regression Statistics Multiple R 0.63 R Square 0.40 Adjusted R Square 0.23 Standard Error 50.00 Observations 15.00 $\text { ANOVA }$ df SS MS F Significance F Regression 3 5994.24 2.40 0.12 Residual 11 27496.82 Total 45479.54 Coefficients Standard Error t Stat P-value Lower 99.0\% Upper 99.0\% Intercept 123.80 48.71 2.54 0.03 -27.47 275.07 AGE -0.82 0.87 -0.95 0.36 -3.51 1.87 TICKETS 21.25 10.66 1.99 0.07 -11.86 54.37 DENSITY -3.14 6.46 -0.49 0.64 -23.19 16.91 -Referring to Table 14-10, to test the significance of the multiple regression model, the p-value of the test statistic in the sample is ________.

TABLE 14-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following 4 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X₁) the amount of insulation in inches (X₂), the number of windows in the house (X₃), and the age of the furnace in years (X₄). Given below are the Excel outputs of two regression models. Model 1 Regression Statistics R Square 0.8080 Adjusted R Square 0.7568 Observations 20 $\mathrm{ANOVA}$ df SS MS F Significance F Regression 4 169503.4241 42375.86 15.7874 0.0000 Residual 15 40262.3259 2684.155 Total 19 209765.75 Coefficients Standard Error t Stat P-value Lower 90.0\% Upper 90.0\% Intercept 421.4277 77.8614 5.4125 0.0000 284.9327 557.9227 (Temperature) -4.5098 0.8129 -5.5476 0.0000 -5.9349 -3.0847 (Insulation) -14.9029 5.0508 -2.9505 0.0099 -23.7573 -6.0485 (Windows) 0.2151 4.8675 0.0442 0.9653 -8.3181 8.7484 (Furnace Age) 6.3780 4.1026 1.5546 0.1408 -0.8140 13.5702 Model 2 Regression Statistics R Square 0.7768 Adjusted R Square 0.7506 Observations 20 $\text { ANOVA }$ Significance df SS MS F F Regression 2 162958.2277 81479.11 29.5923 0.0000 Residual 17 46807.5222 2753.384 Total 19 209765.75 Coefficients Standard Error \ t Stat P-value Lower 95\% Upper 95\% Intercept 489.3227 43.9826 11.1253 0.0000 396.5273 582.1180 (Temperature) -5.1103 0.6951 -7.3515 0.0000 -6.5769 -3.6437 (Insulation) -14.7195 4.8864 -3.0123 0.0078 -25.0290 -4.4099 -Referring to Table 14-6, what is the 90% confidence interval for the expected change in heating costs as a result of a 1 degree Fahrenheit change in the daily minimum outside temperature using Model 1?

TABLE 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending: Regression Statistics Multiple R 0.7930 R Square 0.6288 Adjusted R 0.6029 Square Standard 10.4570 Error Observations 47 $\text { ANOVA }$ df SS MS Significance F Regression 3 7965.08 2655.03 24.2802 0.0000 Residual 43 4702.02 109.35 Total 46 12667.11 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 0.0000 -957.3401 -549.5050 \% Attendance 8.5014 1.0771 7.8929 0.0000 6.3292 10.6735 Salary 0.000000685 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 -Referring to Table 14-15, which of the following is the correct null hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

TABLE 14-5 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT Regression Statistics Multiple R 0.830 R Square 0.689 Adjusted R Square 0.662 Standard Error 17501.643 Observations 26 ANOVA df SS MS F Signif F Regression 2 15579777040 7789888520 25.432 0.0001 Residual 23 7045072780 306307512 Total 25 22624849820 Coeff StdError t Stat p -value Intercept 15800.0000 6038.2999 2.617 0.0154 Capital 0.1245 0.2045 0.609 0.5485 Wages 7.0762 1.4729 4.804 0.0001 -Referring to Table 14-5, what is the p-value for testing whether Capital has a positive influence on corporate sales?

TABLE 14-11 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds). Two variables thought to affect weight-loss are client's length of time on the weight-loss program and time of session. These variables are described below: Y = Weight-loss (in pounds) X₁ = Length of time in weight-loss program (in months) X₂ = 1 if morning session, 0 if not X₃ = 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₁X₂ + β₅X₁X₂ + ε Partial output from Microsoft Excel follows: Regression Statistics Multiple R 0.73514 R Square 0.540438 Adjusted R Square 0.157469 Standard Error 12.4147 Observations 12 ANOVA $F = 5.41118 \quad$ Significance $F = 0.040201$ Coeff StdError t Stat p -value Intercept 0.089744 14.127 0.0060 0.9951 Length 6.22538 2.43473 2.54956 0.0479 Morn Ses 2.217272 22.1416 0.100141 0.9235 Aft Ses 11.8233 3.1545 3.558901 0.0165 Length*Morn Ses 0.77058 3.562 0.216334 0.8359 Length Aft Ses -0.54147 3.35988 -0.161158 0.8773 -Referring to Table 14-11, in terms of the ?s in the model, give the mean change in weight-loss (Y)for every 1 month increase in time in the program (X?)when attending the evening session.

TABLE 14-14 An automotive engineer would like to be able to predict automobile mileages. She believes that the two most important characteristics that affect mileage are horsepower and the number of cylinders (4 or 6) of a car. She believes that the appropriate model is Y = 40 - 0.05X₁ + 20X₂ - 0.1X₁X₂ where X₁ = horsepower X₂ = 1 if 4 cylinders, 0 if 6 cylinders Y = mileage. -Referring to Table 14-14, the fitted model for predicting mileages for 6-cylinder cars is ________.

TABLE 14-3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. SUMMARY OUTPUT Regression Statistics Multiple R 0.991 R Square 0.982 Adjusted R Square 0.976 Standard Error 0.299 Observations 10 ANOVA df SS MS F Signif F Regression 2 33.4163 16.7082 186.325 0.0001 Residual 7 0.6277 0.0897 Total 9 34.0440 Coeff StdError t Stat p -value Intercept -0.0861 0.5674 -0.152 0.8837 GDP 0.7654 0.0574 13.340 0.0001 Price -0.0006 0.0028 -0.219 0.8330 -Referring to Table 14-3, to test whether gross domestic product has a positive impact on consumption, the p-value is

TABLE 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2 Yj. (Allvariables except $j$ ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201. Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations $\text { ANOVA }$ df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40 $\text { ANOVA }$ df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Table 14-17 Model 1, ________ of the variation in the number of weeks a worker is unemployed due to a layoff can be explained by the six independent variables.

TABLE 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending: Regression Statistics Multiple R 0.7930 R Square 0.6288 Adjusted R 0.6029 Square Standard 10.4570 Error Observations 47 $\text { ANOVA }$ df SS MS Significance F Regression 3 7965.08 2655.03 24.2802 0.0000 Residual 43 4702.02 109.35 Total 46 12667.11 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 0.0000 -957.3401 -549.5050 \% Attendance 8.5014 1.0771 7.8929 0.0000 6.3292 10.6735 Salary 0.000000685 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 -Referring to Table 14-15, what is the value of the test statistic when testing whether instructional spending per pupil has any effect on percentage of students passing the proficiency test, taking into account the effect of all the other independent variables?

TABLE 14-5 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT Regression Statistics Multiple R 0.830 R Square 0.689 Adjusted R Square 0.662 Standard Error 17501.643 Observations 26 ANOVA df SS MS F Signif F Regression 2 15579777040 7789888520 25.432 0.0001 Residual 23 7045072780 306307512 Total 25 22624849820 Coeff StdError t Stat p -value Intercept 15800.0000 6038.2999 2.617 0.0154 Capital 0.1245 0.2045 0.609 0.5485 Wages 7.0762 1.4729 4.804 0.0001 -Referring to Table 14-5, one company in the sample had sales of $21.439 billion (Sales = 21,439). This company spent $300 million on capital and $700 million on wages. What is the residual (in millions of dollars)for this data point?

TABLE 14-12 As a project for his business statistics class, a student examined the factors that determined parking meter rates throughout the campus area. Data were collected for the price per hour of parking, blocks to the quadrangle, and one of the three jurisdictions: on campus, in downtown and off campus, or outside of downtown and off campus. The population regression model hypothesized is Yᵢ = α + β₁X₁ᵢ + β₂X₂ᵢ + β₃X₃ᵢ + ε where Y is the meter price X₁ is the number of blocks to the quad X₂ is a dummy variable that takes the value 1 if the meter is located in downtown and off campus and the value 0 otherwise X₃ is a dummy variable that takes the value 1 if the meter is located outside of downtown and off campus, and the value 0 otherwise The following Excel results are obtained. Regression Statistics Multiple R 0.9659 R Square 0.9331 Adjusted R Square 0.9294 Standard Error 0.0327 Observations 58 $\text { ANOVA }$ Df SS MS F Significance F Regression 3 0.8094 0.2698 251.1995 0.0000 Residual 54 0.0580 0.0010 Total 57 0.8675 Coefficient Standard Error S Stat P-value Intercept 0.5118 0.0136 37.4675 2.4904 -0.0045 0.0034 -1.3276 0.1898 -0.2392 0.0123 -19.3942 0.0000 -0.0002 0.0123 -0.0214 0.9829 -Referring to Table 14-12, what is the correct interpretation for the estimated coefficient for X??

TABLE 14-7 The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units (credits) and total SAT scores of each. She takes a sample of students and generates the following Microsoft Excel output: SUMMARY OUTPUT SUMMARY OUTPUT Regression Statistics Multiple R 0.916 R Square 0.839 Adjusted R Square 0.732 Standard Error 0.24685 Observations 6 ANOVA df SS MS F Signif F Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat p -value Intercept 4.593897 1.13374542 4.052 0.0271 Units -0.247270 0.06268485 -3.945 0.0290 SAT Total 0.001443 0.00101241 1.425 0.2494 -Referring to Table 14-7, the department head wants to test H?: ?? = ?? = 0. At a level of significance of 0.05, the null hypothesis is rejected.

TABLE 14-19 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0) and 15 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Atitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age). The Minitab output is given below: Logistic Regression Table Odds 95\% CI Predictor Coef SE Coef Z P Ratio Lower Upper Constant -70.49 47.22 -1.49 0.135 Income 0.2868 0.1523 1.88 0.060 1.33 0.99 1.80 LawnSiz 1.0647 0.7472 1.42 0.154 2.90 0.67 12.54 Attitude -12.744 9.455 -1.35 0.178 0.00 0.00 326.06 Teenager -0.200 1.061 -0.19 0.850 0.82 0.10 6.56 Age 1.0792 0.8783 1.23 0.219 2.94 0.53 16.45 Log-Likelihood $= - 4.890$ Test that all slopes are zero: $\mathrm { G } = 31.808 , \mathrm { DF } = 5 , p$ -value $= 0.000$ Goodness-of-Fit Tests Method Chi-Square DF Pearson 9.313 24 0.997 Deviance 9.780 24 0.995 Hosmer-Lemeshow 0.571 8 1.000 -Referring to Table 14-19, there is not enough evidence to conclude that the model is not a good-fitting model at a 0.05 level of significance.

TABLE 14-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following 4 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X₁) the amount of insulation in inches (X₂), the number of windows in the house (X₃), and the age of the furnace in years (X₄). Given below are the Excel outputs of two regression models. Model 1 Regression Statistics R Square 0.8080 Adjusted R Square 0.7568 Observations 20 $\mathrm{ANOVA}$ df SS MS F Significance F Regression 4 169503.4241 42375.86 15.7874 0.0000 Residual 15 40262.3259 2684.155 Total 19 209765.75 Coefficients Standard Error t Stat P-value Lower 90.0\% Upper 90.0\% Intercept 421.4277 77.8614 5.4125 0.0000 284.9327 557.9227 (Temperature) -4.5098 0.8129 -5.5476 0.0000 -5.9349 -3.0847 (Insulation) -14.9029 5.0508 -2.9505 0.0099 -23.7573 -6.0485 (Windows) 0.2151 4.8675 0.0442 0.9653 -8.3181 8.7484 (Furnace Age) 6.3780 4.1026 1.5546 0.1408 -0.8140 13.5702 Model 2 Regression Statistics R Square 0.7768 Adjusted R Square 0.7506 Observations 20 $\text { ANOVA }$ Significance df SS MS F F Regression 2 162958.2277 81479.11 29.5923 0.0000 Residual 17 46807.5222 2753.384 Total 19 209765.75 Coefficients Standard Error \ t Stat P-value Lower 95\% Upper 95\% Intercept 489.3227 43.9826 11.1253 0.0000 396.5273 582.1180 (Temperature) -5.1103 0.6951 -7.3515 0.0000 -6.5769 -3.6437 (Insulation) -14.7195 4.8864 -3.0123 0.0078 -25.0290 -4.4099 -Referring to Table 14-6, what can we say about Model 1?

TABLE 14-3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. SUMMARY OUTPUT Regression Statistics Multiple R 0.991 R Square 0.982 Adjusted R Square 0.976 Standard Error 0.299 Observations 10 ANOVA df SS MS F Signif F Regression 2 33.4163 16.7082 186.325 0.0001 Residual 7 0.6277 0.0897 Total 9 34.0440 Coeff StdError t Stat p -value Intercept -0.0861 0.5674 -0.152 0.8837 GDP 0.7654 0.0574 13.340 0.0001 Price -0.0006 0.0028 -0.219 0.8330 -Referring to Table 14-3, when the economist used a simple linear regression model with consumption as the dependent variable and GDP as the independent variable, he obtained an r² value of 0.971. What additional percentage of the total variation of consumption has been explained by including aggregate prices in the multiple regression?