Exam 14: Introduction to Multiple Regression
Exam 1: Introduction145 Questions
Exam 2: Organizing and Visualizing Data210 Questions
Exam 3: Numerical Descriptive Measures153 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions218 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions191 Questions
Exam 7: Sampling and Sampling Distributions197 Questions
Exam 8: Confidence Interval Estimation196 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests165 Questions
Exam 10: Two-Sample Tests210 Questions
Exam 11: Analysis of Variance213 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests201 Questions
Exam 13: Simple Linear Regression213 Questions
Exam 14: Introduction to Multiple Regression355 Questions
Exam 15: Multiple Regression Model Building96 Questions
Exam 16: Time-Series Forecasting168 Questions
Exam 17: Statistical Applications in Quality Management133 Questions
Exam 18: A Roadmap for Analyzing Data54 Questions
Select questions type
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below: Logistic Regression Table
Odds 95\% Predictor Coef SE Coef Ratio Lower Upper Constant -27.118 6.696 -4.05 0.000 SAT 0.015 0.004666 3.17 0.002 1.01 1.01 1.02 Toefl550 -0.390 0.9538 -0.41 0.682 0.68 0.10 4.39 Room/Brd 2.078 0.5076 4.09 0.000 7.99 2.95 21.60
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF P Pearson 143.551 76 0.000 Deviance 43.767 76 0.999 Hosmer-Lemeshow 15.731 8 0.046
-Referring to Table 14-18, what is the estimated probability that a school with an mean SAT score of 1100, a TOEFL criterion that is not at least 550, and the room and board expense of 7 thousand dollars will be a private school?
(Short Answer)
4.9/5  (35)
(35)
TABLE 14-19
The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0) and 15 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Atitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age).
The Minitab output is given below: Logistic Regression Table
Odds 95\% CI Predictor Coef SE Coef Z P Ratio Lower Upper Constant -70.49 47.22 -1.49 0.135 Income 0.2868 0.1523 1.88 0.060 1.33 0.99 1.80 LawnSiz 1.0647 0.7472 1.42 0.154 2.90 0.67 12.54 Attitude -12.744 9.455 -1.35 0.178 0.00 0.00 326.06 Teenager -0.200 1.061 -0.19 0.850 0.82 0.10 6.56 Age 1.0792 0.8783 1.23 0.219 2.94 0.53 16.45
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF Pearson 9.313 24 0.997 Deviance 9.780 24 0.995 Hosmer-Lemeshow 0.571 8 1.000
-Referring to Table 14-19, what should be the decision ('reject' or 'do not reject')on the null hypothesis when testing whether Income makes a significant contribution to the model in the presence of the other independent variables at a 0.05 level of significance?
(Short Answer)
4.9/5  (27)
(27)
TABLE 14-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2
Yj. (Allvariables except ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations
df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40
df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9
Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Table 14-17 Model 1, there is sufficient evidence that all of the explanatory variables are related to the number of weeks a worker is unemployed due to a layoff at a 10% level of significance.
(True/False)
4.9/5  (31)
(31)
TABLE 14-19
The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0) and 15 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Atitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age).
The Minitab output is given below: Logistic Regression Table
Odds 95\% CI Predictor Coef SE Coef Z P Ratio Lower Upper Constant -70.49 47.22 -1.49 0.135 Income 0.2868 0.1523 1.88 0.060 1.33 0.99 1.80 LawnSiz 1.0647 0.7472 1.42 0.154 2.90 0.67 12.54 Attitude -12.744 9.455 -1.35 0.178 0.00 0.00 326.06 Teenager -0.200 1.061 -0.19 0.850 0.82 0.10 6.56 Age 1.0792 0.8783 1.23 0.219 2.94 0.53 16.45
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF Pearson 9.313 24 0.997 Deviance 9.780 24 0.995 Hosmer-Lemeshow 0.571 8 1.000
-Referring to Table 14-19, the null hypothesis that the model is a good-fitting model cannot be rejected when allowing for a 5% probability of making a type I error.
(True/False)
4.8/5  (29)
(29)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
Regression Statistics Multiple R 0.7930 R Square 0.6288 Adjusted R 0.6029 Square Standard 10.4570 Error Observations 47
df SS MS Significance F Regression 3 7965.08 2655.03 24.2802 0.0000 Residual 43 4702.02 109.35 Total 46 12667.11
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 0.0000 -957.3401 -549.5050 \% Attendance 8.5014 1.0771 7.8929 0.0000 6.3292 10.6735 Salary 0.000000685 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153
-Referring to Table 14-15, predict the percentage of students passing the proficiency test for a school which has a daily mean of 95% of students attending class, a mean teacher salary of 40,000 dollars, and an instructional spending per pupil of 2,000 dollars.
(Short Answer)
4.8/5  (45)
(45)
TABLE 14-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size), and education of the head of household (School). House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: SUMMARY OUTPUT
Regression Statistics
Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50
ANOVA
df SS MS F Signif F Regression 3605.7736 1201.9245 0.0000 Residual 1214.2264 26.3962 Total 49 4820.0000
Coeff StdError t Stat p -value Intercept -1.6335 5.8078 -0.281 0.7798 Income 0.4485 0.1137 3.9545 0.0003 Size 4.2615 0.8062 5.286 0.0001 School -0.6517 0.4319 -1.509 0.1383
-Referring to Table 14-4, suppose the builder wants to test whether the coefficient on Income is significantly different from 0. What is the value of the relevant t-statistic?
(Multiple Choice)
4.9/5  (27)
(27)
TABLE 14-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2
Yj. (Allvariables except ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations
df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40
df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9
Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Table 14-17 and using both Model 1 and Model 2, the null hypothesis for testing whether the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable should be rejected at a 5% level of significance?
(True/False)
4.8/5  (31)
(31)
TABLE 14-16
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
Regression Statistics Multiple R 0.8013 R Square 0.6421 Adjusted R Square 0.6313 Standard Error 1.0507 Observations 171
df SS MS F Significance F Regression 5 326.8700 65.3740 59.2168 0.0000 Residual 165 182.1564 1.1040 Total 170 509.0263
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 12.8627 1.0927 11.7713 0.0000 10.7052 15.0202 Cargo Vol 0.0259 0.0102 2.5518 0.0116 0.0059 0.0460 HP -0.0200 0.0018 -11.3307 0.0000 -0.0235 -0.0165 MPG -0.0620 0.0303 -2.0464 0.0423 -0.1218 -0.0022 SUV 0.7679 0.4314 1.7802 0.0769 -0.0838 1.6196 Sedan 0.6427 0.2790 2.3034 0.0225 0.0918 1.1935
The various residual plots are as shown below.
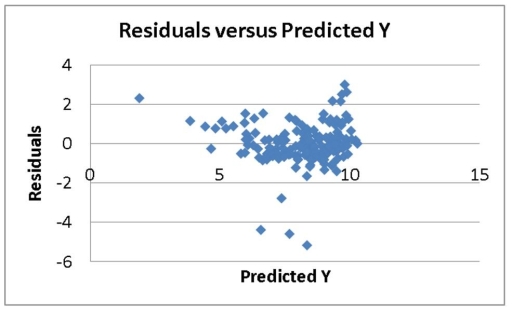
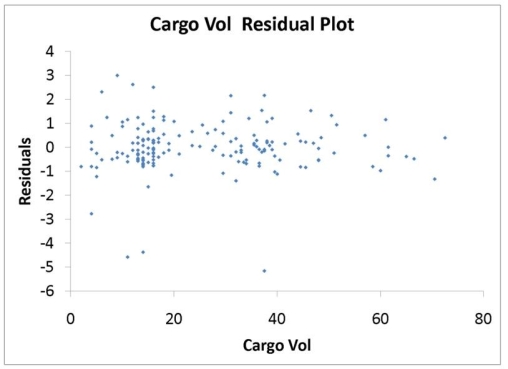
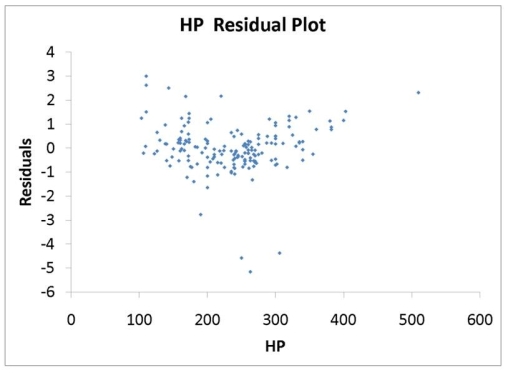
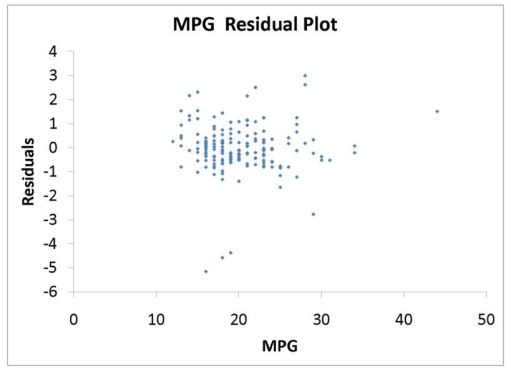
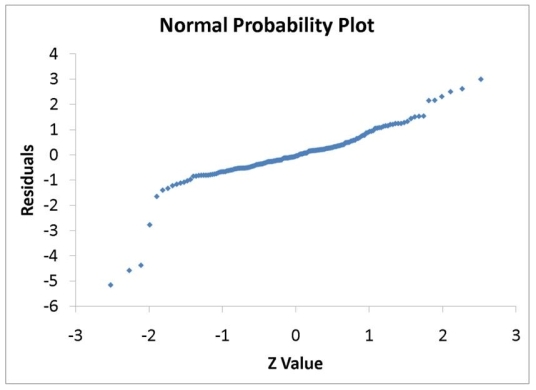 The coefficients of partial determination . (All variables except of each of the 5 predictors are, respectively, , and .
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other variables as independent variables are, respectively, .
-Referring to 14-16, the 0 to 60 miles per hour acceleration time of a coupe is predicted to be 0.7679 seconds higher than that of a sedan.
The coefficients of partial determination . (All variables except of each of the 5 predictors are, respectively, , and .
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other variables as independent variables are, respectively, .
-Referring to 14-16, the 0 to 60 miles per hour acceleration time of a coupe is predicted to be 0.7679 seconds higher than that of a sedan.
(True/False)
4.9/5  (38)
(38)
TABLE 14-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2
Yj. (Allvariables except ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations
df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40
df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9
Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Table 14-17 Model 1, estimate the mean number of weeks being unemployed due to a layoff for a worker who is a thirty-year old, has 10 years of education, has 15 years of experience at the previous job, is married, is the head of household and is a manager.
(Short Answer)
4.7/5  (27)
(27)
TABLE 14-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics Multiple R 0.830 R Square 0.689 Adjusted R Square 0.662 Standard Error 17501.643 Observations 26
ANOVA
df SS MS F Signif F Regression 2 15579777040 7789888520 25.432 0.0001 Residual 23 7045072780 306307512 Total 25 22624849820
Coeff StdError t Stat p -value Intercept 15800.0000 6038.2999 2.617 0.0154 Capital 0.1245 0.2045 0.609 0.5485 Wages 7.0762 1.4729 4.804 0.0001
-Referring to Table 14-5, what is the p-value for Capital?
(Multiple Choice)
4.8/5  (34)
(34)
Multiple regression is the process of using several independent variables to predict a number of dependent variables.
(True/False)
4.8/5  (32)
(32)
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below: Logistic Regression Table
Odds 95\% Predictor Coef SE Coef Ratio Lower Upper Constant -27.118 6.696 -4.05 0.000 SAT 0.015 0.004666 3.17 0.002 1.01 1.01 1.02 Toefl550 -0.390 0.9538 -0.41 0.682 0.68 0.10 4.39 Room/Brd 2.078 0.5076 4.09 0.000 7.99 2.95 21.60
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF P Pearson 143.551 76 0.000 Deviance 43.767 76 0.999 Hosmer-Lemeshow 15.731 8 0.046
-Referring to Table 14-18, which of the following is the correct interpretation for the SAT slope coefficient?
(Multiple Choice)
4.9/5  (37)
(37)
TABLE 14-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size), and education of the head of household (School). House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: SUMMARY OUTPUT
Regression Statistics
Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50
ANOVA
df SS MS F Signif F Regression 3605.7736 1201.9245 0.0000 Residual 1214.2264 26.3962 Total 49 4820.0000
Coeff StdError t Stat p -value Intercept -1.6335 5.8078 -0.281 0.7798 Income 0.4485 0.1137 3.9545 0.0003 Size 4.2615 0.8062 5.286 0.0001 School -0.6517 0.4319 -1.509 0.1383
-Referring to Table 14-4, one individual in the sample had an annual income of $40,000, a family size of 1, and an education of 8 years. This individual owned a home with an area of 1,000 square feet (House = 10.00). What is the residual (in hundreds of square feet)for this data point?
(Multiple Choice)
4.9/5  (31)
(31)
TABLE 14-7
The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units (credits) and total SAT scores of each. She takes a sample of students and generates the following Microsoft Excel output:
SUMMARY OUTPUT
SUMMARY OUTPUT
Regression Statistics Multiple R 0.916 R Square 0.839 Adjusted R Square 0.732 Standard Error 0.24685 Observations 6
ANOVA
df SS MS F Signif F Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500
Coeff StdError t Stat p -value Intercept 4.593897 1.13374542 4.052 0.0271 Units -0.247270 0.06268485 -3.945 0.0290 SAT Total 0.001443 0.00101241 1.425 0.2494
-Referring to Table 14-7, the department head wants to use a t test to test for the significance of the coefficient of X₁. The value of the test statistic is ________.
(Short Answer)
4.9/5  (31)
(31)
TABLE 14-14
An automotive engineer would like to be able to predict automobile mileages. She believes that the two most important characteristics that affect mileage are horsepower and the number of cylinders (4 or 6) of a car. She believes that the appropriate model is
Y = 40 - 0.05X₁ + 20X₂ - 0.1X₁X₂
where X₁ = horsepower
X₂ = 1 if 4 cylinders, 0 if 6 cylinders
Y = mileage.
-Referring to Table 14-14, the predicted mileage for a 200 horsepower, 4-cylinder car is ________.
(Short Answer)
4.7/5  (41)
(41)
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below: Logistic Regression Table
Odds 95\% Predictor Coef SE Coef Ratio Lower Upper Constant -27.118 6.696 -4.05 0.000 SAT 0.015 0.004666 3.17 0.002 1.01 1.01 1.02 Toefl550 -0.390 0.9538 -0.41 0.682 0.68 0.10 4.39 Room/Brd 2.078 0.5076 4.09 0.000 7.99 2.95 21.60
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF P Pearson 143.551 76 0.000 Deviance 43.767 76 0.999 Hosmer-Lemeshow 15.731 8 0.046
-Referring to Table 14-18, what should be the decision ('reject' or 'do not reject')on the null hypothesis when testing whether Toefl500 makes a significant contribution to the model in the presence of the other independent variables at a 0.05 level of significance?
(Short Answer)
4.7/5  (39)
(39)
TABLE 14-1
A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X₁) and how he/she scored on a business aptitude test (X₂). A random sample of 8 employees provides the following: 1 100 10 7 2 90 3 10 3 80 8 9 4 70 5 4 5 60 5 8 6 50 7 5 7 40 1 4 8 30 1 1
-Referring to Table 14-1, for these data, what is the value for the regression constant, b??
(Multiple Choice)
4.9/5  (39)
(39)
TABLE 14-18
A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college, the room and board expense measured in thousands of dollars (Room/Brd), and whether the TOEFL criterion is at least 550 (Toefl550 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise).
The Minitab output is given below: Logistic Regression Table
Odds 95\% Predictor Coef SE Coef Ratio Lower Upper Constant -27.118 6.696 -4.05 0.000 SAT 0.015 0.004666 3.17 0.002 1.01 1.01 1.02 Toefl550 -0.390 0.9538 -0.41 0.682 0.68 0.10 4.39 Room/Brd 2.078 0.5076 4.09 0.000 7.99 2.95 21.60
Log-Likelihood
Test that all slopes are zero: -value
Goodness-of-Fit Tests
Method Chi-Square DF P Pearson 143.551 76 0.000 Deviance 43.767 76 0.999 Hosmer-Lemeshow 15.731 8 0.046
-Referring to Table 14-18, what should be the decision ('reject' or 'do not reject')on the null hypothesis when testing whether SAT makes a significant contribution to the model in the presence of the other independent variables at a 0.05 level of significance?
(Short Answer)
4.9/5  (38)
(38)
TABLE 14-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. The coefficients of partial determination ( 2
Yj. (Allvariables except ) ) of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
Regression Statistics Multiple R 0.7035 R Square 0.4949 Adjusted R 0.4030 Square Standard 18.4861 Error 40 Observations
df SS MS F significance F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 22325.9
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are
Age and Manager. The results of the regression analysis are given below:
Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R 0.3765 Square Standard Error 18.8929 Observations 40
df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9
Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Table 14-17 and using both Model 1 and Model 2, what is the value of the test statistic for testing whether the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable at a 5% level of significance?
(Short Answer)
4.8/5  (43)
(43)
TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:
Regression Statistics Multiple R 0.7930 R Square 0.6288 Adjusted R 0.6029 Square Standard 10.4570 Error Observations 47
df SS MS Significance F Regression 3 7965.08 2655.03 24.2802 0.0000 Residual 43 4702.02 109.35 Total 46 12667.11
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 0.0000 -957.3401 -549.5050 \% Attendance 8.5014 1.0771 7.8929 0.0000 6.3292 10.6735 Salary 0.000000685 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153
-Referring to Table 14-15, what are the numerator and denominator degrees of freedom, respectively, for the test statistic to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
(Short Answer)
4.9/5  (34)
(34)
Showing 121 - 140 of 355
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)