Exam 9: Discrete Mathematics
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find the coefficient of the given term in the binomial expansion.
- term,
(Multiple Choice)
4.9/5  (44)
(44)
Solve.
-How many different three-digit numbers can be written using digits from the set {5, 6, 7, 8, 9} without any repeating digits?
(Multiple Choice)
4.7/5  (36)
(36)
Find the coefficient of the given term in the binomial expansion.
- term,
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the infinite geometric series converges. If the series converges, determine the limit.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the sum of the first n terms of the sequence.
-10, 2, -6, -14, . . . ; n = 12
(Multiple Choice)
4.8/5  (32)
(32)
In how many ways can you answer the questions on an exam that consists of 8 multiple choice questions, each of which has 4 answer choices, followed by 5 true-false questions?
(Multiple Choice)
4.9/5  (33)
(33)
Write the sum using summation notation, assuming the suggested pattern continues.
-
(Multiple Choice)
4.8/5  (31)
(31)
Find an explicit rule for the nth term of the arithmetic sequence.
-
(Multiple Choice)
4.9/5  (40)
(40)
Construct a graph for the first ten terms of the sequence.
-
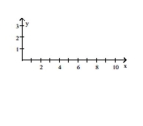
(Multiple Choice)
4.7/5  (48)
(48)
Use mathematical induction to prove the statement is true for all positive integers n.
-6 + 12 + 18 + ... + 6n = 3n(n + 1)
(Essay)
4.7/5  (36)
(36)
Showing 101 - 120 of 154
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)