Exam 8: Analytic Geometry in Two and Three Dimensions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Solve the problem.
-A rectangular board is 14 by 20 units. How far from the short side of the board will the foci be located to determine the largest elliptical tabletop?
(Multiple Choice)
4.8/5  (37)
(37)
A quadratic equation has been transformed using the rotation equations x = 0.8u - 0.6v and y = 0.6u + 0.8v.
Convert the given point from (u, v) coordinates back to (x, y) coordinates.
-hyperbola foci
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A railroad tunnel is shaped like a semiellipse. The height of the tunnel at the center is and the vertical clearance must be at a point from the center. Find an equation for the ellipse.
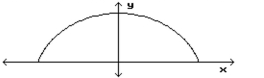
(Multiple Choice)
4.8/5  (32)
(32)
Find the standard form of the equation of the parabola.
-Focus at , directrix
(Multiple Choice)
4.7/5  (38)
(38)
Find parametric equations for the line described below.
-The line through the point in the direction of the vector
(Multiple Choice)
4.8/5  (33)
(33)
Showing 81 - 100 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)