Exam 8: Analytic Geometry in Two and Three Dimensions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find an equation in standard form for the ellipse that satisfies the given conditions.
-An ellipse with foci at and ; major axis length of 10
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Find the vector equation of the line through and .
(Multiple Choice)
4.9/5  (31)
(31)
Use the discriminant to decide whether the equation represents a parabola, an ellipse, or a hyperbola.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find parametric equations for the line described below.
-The line through the points and
(Multiple Choice)
4.9/5  (32)
(32)
Find the center, vertices, and foci of the ellipse with the given equation.
-
(Multiple Choice)
4.8/5  (31)
(31)
Find an equation in standard form for the ellipse that satisfies the given conditions.
-Major axis endpoints , minor axis length 10
(Multiple Choice)
4.8/5  (40)
(40)
Find an equation in standard form for the ellipse that satisfies the given conditions.
-An ellipse with intercepts and , center at origin
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-The roof of a building is in the shape of the hyperbola , where and are in meters. Determine the distance, w, the outside walls are apart, if the height of each wall is .
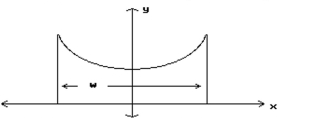
(Multiple Choice)
4.9/5  (45)
(45)
Find the standard form of the equation of the parabola.
-Focus at , directrix
(Multiple Choice)
4.9/5  (42)
(42)
Find the standard form of the equation of the parabola.
-Vertex at the origin, focus at
(Multiple Choice)
5.0/5  (48)
(48)
Showing 121 - 140 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)