Exam 3: Exponential, Logistic, and Logarithmic Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Solve the problem.
-How long will it take for $1100 to grow to $4800 at an interest rate of 10.9% if the interest is compounded quarterly? Round the number of years to the nearest hundredth.
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Estimate the -value associated with as predicted by the natural logarithmic regression equation for the following data.

(Multiple Choice)
4.7/5  (26)
(26)
State whether the function is an exponential growth function or exponential decay function, and describe its end
behavior using limits.
-
(Multiple Choice)
4.7/5  (33)
(33)
Find the following using a calculator. Round to four decimal places.
-
(Multiple Choice)
5.0/5  (34)
(34)
Solve the problem.
-Matthew obtains a 30-year $84,000 house loan with an APR of 7.23%. What is his monthly payment?
(Multiple Choice)
4.9/5  (35)
(35)
Describe how to transform the graph of the basic function g(x) into the graph of the given function f(x).
-
(Multiple Choice)
4.8/5  (37)
(37)
Provide an appropriate response.
-
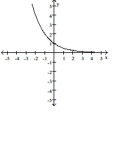 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and : of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and : of .
(Essay)
4.7/5  (29)
(29)
Solve the problem.
-The table shows the population of a certain city in various years. The data can be modeled by an exponential function of the form . Use exponential regression to predict the population of the city in the year 2000 . (You will first need to determine the exponential function that models this data).
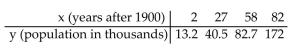
(Multiple Choice)
4.8/5  (34)
(34)
State whether the function is an exponential growth function or exponential decay function, and describe its end
behavior using limits.
-
(Multiple Choice)
5.0/5  (36)
(36)
Decide whether the function is an exponential growth or exponential decay function and find the constant percentage
rate of growth or decay.
-
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-The table shows the number of sales of scooters , in thousands, months after they are introduced on the market. Use regression to find a logistic function that models this data. Round the constants to the nearest hundredth.

(Multiple Choice)
4.7/5  (38)
(38)
Graph the function and analyze it for domain, range, continuity, increasing or decreasing behavior, asymptotes, and end
behavior.
-f(x) = log3(6x)
(Essay)
4.8/5  (35)
(35)
Solve the problem.
-By how many orders of magnitude do a $20 bill and a nickel differ?
(Multiple Choice)
4.7/5  (31)
(31)
Showing 181 - 200 of 350
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)