Exam 3: Exponential, Logistic, and Logarithmic Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Graph the function and analyze it for domain, range, continuity, increasing or decreasing behavior, symmetry,
boundedness, extrema, asymptotes, and end behavior.
-
(Essay)
4.8/5  (32)
(32)
Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of
logarithms or multiples of logarithms.
-
(Multiple Choice)
4.9/5  (34)
(34)
Graph the function and analyze it for domain, range, continuity, increasing or decreasing behavior, symmetry,
boundedness, extrema, asymptotes, and end behavior.
-
(Essay)
4.7/5  (36)
(36)
Use a calculator to find an approximate solution to the equation.
-
(Multiple Choice)
5.0/5  (36)
(36)
Determine the function which corresponds to the given graph.
-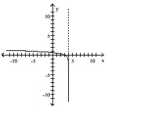 The asymptote is
The asymptote is
(Multiple Choice)
4.8/5  (23)
(23)
Graph the function and analyze it for domain, range, continuity, increasing or decreasing behavior, asymptotes, and end
behavior.
-f(x) = log1/2(x - 1)
(Essay)
4.8/5  (29)
(29)
Determine a formula for the exponential function.
-The graph of an exponential function is given. Which of the following is the correct equation of the function?
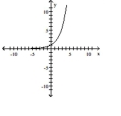
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-In September 1998 the population of the country of West Goma in millions was modeled by . At the same time the population of East Goma in millions was modeled by . In both formulas is the year, where corresponds to September 1998. Assuming these trends continue, estimate the year when the population of West Goma will equal the population of East Goma.
(Multiple Choice)
4.9/5  (33)
(33)
Find the amount accumulated after investing a principal P for t years at an interest rate r.
-P = $800, t = 4, r = 1% compounded continuously
(Multiple Choice)
4.9/5  (39)
(39)
Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of
logarithms or multiples of logarithms.
-
(Multiple Choice)
4.9/5  (30)
(30)
Decide if the function is an exponential function. If it is, state the initial value and the base.
-
(Multiple Choice)
4.8/5  (35)
(35)
Use the change of base rule to find the logarithm to four decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
Showing 61 - 80 of 350
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)