Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (38)
(38)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.7/5  (41)
(41)
Find the absolute extreme values of the function on the interval.
-g(x) = -x2 + 8x - 16, 4 x 4
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-A trucker handed in a ticket at a toll booth showing that in 3 hours he had covered 222 miles on a toll road with speed limit 65 mph. The trucker was cited for speeding. Why?
(Essay)
4.9/5  (37)
(37)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
5.0/5  (32)
(32)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-Imagine there is a function for which f'(x) = 0 for all x. Does such a function exist? Is it reasonable to say that all values of x are critical points for such a function? Is it reasonable to say that all values of x are extreme values for such a function. Give reasons for your answer.
(Essay)
4.9/5  (34)
(34)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
5.0/5  (36)
(36)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time t, find the body's positios .
(Multiple Choice)
4.7/5  (26)
(26)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-Let
(a) Does exist?
(b) Does exist?
(c) Does exist?
(d) Determine all extrema of .
(Essay)
4.9/5  (36)
(36)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
- ,
(True/False)
4.9/5  (30)
(30)
Find the location of the indicated absolute extremum for the function.
-Maximum 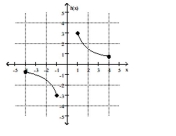
(Multiple Choice)
4.9/5  (30)
(30)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (48)
(48)
Solve the problem.
-A rocket lifts off the surface of Earth with a constant acceleration of 30 m/sec2. How fast will the rocket be going 2.5 minutes later?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-At about what velocity do you enter the water if you jump from a cliff? (Use .)
(Multiple Choice)
4.8/5  (34)
(34)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.9/5  (38)
(38)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
- Round to the nearest thousandth.
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-Given the acceleration, initial velocity, and initial position of a body moving along a coordinate line at time , fint body's position at time .
(Multiple Choice)
4.7/5  (36)
(36)
Showing 41 - 60 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)