Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.9/5  (37)
(37)
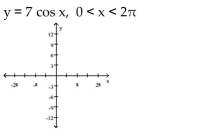
Sketch the graph of the function and determine whether it has any absolute extreme values on its domain.
-
(Multiple Choice)
4.9/5  (29)
(29)
Use the following function and a graphing calculator to answer the questions.
a). Plot the function over the interval to see its general behavior there. Sketch the graph below.
![Use the following function and a graphing calculator to answer the questions. f ( x ) = x ^ { 4 } - 4 x ^ { 2 } + 3 x + 2 , [ - 0.5,1.8 ] a). Plot the function over the interval to see its general behavior there. Sketch the graph below. b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f' as well. List the points as ordered pairs (x, y). c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y). d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y). e). Find the function's absolute extreme values on the interval and identify where they occur.](https://storage.examlex.com/TB8583/11ece0bf_ad47_ecdd_8008_910614b70df5_TB8583_11.jpg) b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f' as well. List the points as ordered pairs (x, y).
c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f' as well. List the points as ordered pairs (x, y).
c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
(Essay)
4.9/5  (34)
(34)
Solve the problem.
-A marathoner ran the 26.2 mile New York City Marathon in 2.7 hrs. Did the runner ever exceed a speed of 9 miles per hour?
(Essay)
4.9/5  (40)
(40)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.8/5  (46)
(46)
Find the location of the indicated absolute extremum for the function.
-Maximum 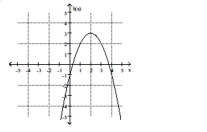
(Multiple Choice)
4.8/5  (44)
(44)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.9/5  (39)
(39)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.7/5  (37)
(37)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.7/5  (31)
(31)
Find the location of the indicated absolute extremum for the function.
-Maximum 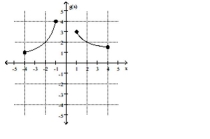
(Multiple Choice)
4.7/5  (43)
(43)
Find the location of the indicated absolute extremum for the function.
-Minimum 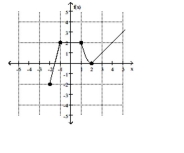
(Multiple Choice)
4.8/5  (47)
(47)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-
(True/False)
4.8/5  (35)
(35)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (35)
(35)
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB8583/11eb8c85_25d9_9f8d_8371_b77a30d12bed_TB8583_00.jpg)
(Multiple Choice)
4.7/5  (31)
(31)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Find the graph that matches the given table.
() -1 0 1 does not exist 3 0
(Multiple Choice)
4.8/5  (33)
(33)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.9/5  (48)
(48)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
5.0/5  (34)
(34)
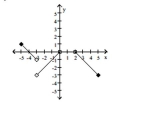
Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.8/5  (33)
(33)
Showing 61 - 80 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)