Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB8583/11eb8c85_25d9_2a59_8371_4b07677186ec_TB8583_00.jpg)
(Multiple Choice)
4.8/5  (37)
(37)
Graph the function, then find the extreme values of the function on the interval and indicate where they occur.
- on the interval -5< x<5
(Multiple Choice)
4.8/5  (48)
(48)
Solve the problem.
-The acceleration of gravity near the surface of Mars is 3.72 m/sec2. If a rock is blasted straight up from the surface with an initial velocity of 85 m/sec (about 190 mph), how high does it go? (Hint: When is velocity zero?)
(Multiple Choice)
4.8/5  (47)
(47)
Using the derivative of f(x) given below, determine the critical points of f(x).
-
(Multiple Choice)
4.9/5  (40)
(40)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.7/5  (42)
(42)
Find the location of the indicated absolute extremum for the function.
-Minimum 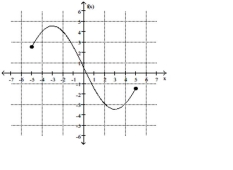
(Multiple Choice)
4.7/5  (33)
(33)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.7/5  (39)
(39)
Provide an appropriate response.
-Suppose that g(0) = 8 and that g'(t) = 4 for all t. Must g(t) = 4t + 8 for all t?
(Essay)
4.8/5  (45)
(45)
Plot the zeros of the given polynomial on the number line together with the zeros of the first derivative.
-

(Multiple Choice)
5.0/5  (35)
(35)
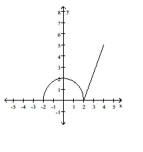
Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.8/5  (38)
(38)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (41)
(41)
Plot the zeros of the given polynomial on the number line together with the zeros of the first derivative.
-

(Multiple Choice)
4.8/5  (38)
(38)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.9/5  (44)
(44)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (40)
(40)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-If the derivative of an odd function g(x) is zero at x = c, can anything be said about the value of g' at x = -c? Give reasons for you answer.
(Essay)
4.8/5  (39)
(39)
Showing 21 - 40 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)