Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Using the derivative of f(x) given below, determine the critical points of f(x).
-
(Multiple Choice)
4.9/5  (42)
(42)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.7/5  (36)
(36)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
- ,
(True/False)
4.8/5  (37)
(37)
Using the derivative of f(x) given below, determine the critical points of f(x).
-f'(x) = (x + 2)(x + 9)
(Multiple Choice)
4.7/5  (44)
(44)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.9/5  (45)
(45)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A particle moves on a coordinate line with acceleration , subject to the conditions that and when . Find the velocity in terms of and the position in terms of .
(Multiple Choice)
4.9/5  (24)
(24)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.7/5  (42)
(42)
Graph the function, then find the extreme values of the function on the interval and indicate where they occur.
-y = - on the interval -2 < x < 7
(Multiple Choice)
4.7/5  (42)
(42)
Find the location of the indicated absolute extremum for the function.
-Minimum 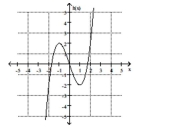
(Multiple Choice)
4.9/5  (35)
(35)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-Find the table that matches the given graph. 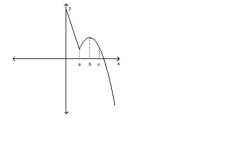
(Multiple Choice)
4.8/5  (38)
(38)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.7/5  (37)
(37)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-f(r) = (r - 7) 3
(Multiple Choice)
4.7/5  (48)
(48)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time t, find the body's positiol .
(Multiple Choice)
4.7/5  (33)
(33)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (40)
(40)
Showing 141 - 159 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)