Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (39)
(39)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-An approximation to the total profit (in thousands of dollars) from the sale of hundred thousand tires is given by . Find the number of hundred thousands of tires that must be sold to maximize profit.
(Multiple Choice)
4.7/5  (39)
(39)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.8/5  (38)
(38)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
4.9/5  (35)
(35)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.9/5  (44)
(44)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.7/5  (34)
(34)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (40)
(40)
Show that the function has exactly one zero in the given interval.
-
(Essay)
4.8/5  (45)
(45)
Using the derivative of f(x) given below, determine the critical points of f(x).
-f'(x) = (x - 5) e-x
(Multiple Choice)
4.9/5  (43)
(43)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-
(True/False)
4.7/5  (36)
(36)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (44)
(44)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
4.9/5  (39)
(39)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (44)
(44)
Provide an appropriate response.
-The function is zero at and and differentiable on , but its derivative on is never zero. Does this example contradict Rolle's Theorem?
(Essay)
4.7/5  (32)
(32)
Find the location of the indicated absolute extremum for the function.
-Minimum 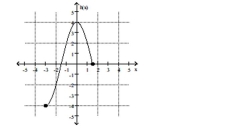
(Multiple Choice)
4.8/5  (34)
(34)
Showing 101 - 120 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)