Exam 5: Analytic Trigonometry
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Use the graph of the function to approximate the maximum points of the graph in the interval . Round your answer to one decimal.
![Use the graph of the function f ( x ) = - 2 \cos ( x ) + \sin ( x ) to approximate the maximum points of the graph in the interval [ 0,2 \pi ] . Round your answer to one decimal.](https://storage.examlex.com/TB8201/11ecdf1f_ae6e_30d7_b402_8f75402b8070_TB8201_11.jpg)
(Multiple Choice)
4.9/5  (38)
(38)
Factor; then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.7/5  (43)
(43)
Find the exact value of the given expression using a sum or difference formula.
(Multiple Choice)
4.9/5  (39)
(39)
Use fundamental identities to simplify the expression below and then determine which of the following is not equivalent.
(Multiple Choice)
4.9/5  (34)
(34)
The rate of change of the function
is given by the expression
Which of the following is its simplification?
(Multiple Choice)
4.9/5  (44)
(44)
Use the sum-to-product formulas to write the given expression as a product.
(Multiple Choice)
4.9/5  (38)
(38)
Find the exact value of given that and . (Both and are in Quadrant II.)
(Multiple Choice)
4.9/5  (42)
(42)
Use the graph below of the function to approximate the solutions to in the interval . Round your answers to one decimal.
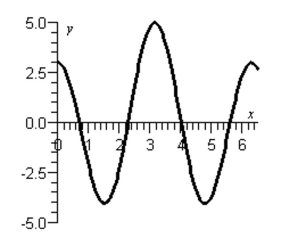
(Multiple Choice)
4.9/5  (38)
(38)
Find all solutions of the following equation on the interval .
(Multiple Choice)
4.7/5  (36)
(36)
Find the exact value of the given expression using a sum or difference formula.
(Multiple Choice)
4.8/5  (40)
(40)
Find the exact value of given that and . (Both and are in Quadrant II.)
(Multiple Choice)
5.0/5  (39)
(39)
Use the product-to-sum formula to write the given product as a sum or difference.
(Multiple Choice)
4.7/5  (37)
(37)
Showing 41 - 60 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)