Exam 1: Functions and Models
Exam 1: Functions and Models112 Questions
Exam 2: Limits and Derivatives76 Questions
Exam 3: Differentiation Rules75 Questions
Exam 4: Applications of Differentiation77 Questions
Exam 5: Integrals60 Questions
Exam 6: Applications of Integration78 Questions
Exam 7: Techniques of Integration79 Questions
Exam 8: Further Applications of Integration59 Questions
Exam 9: Differential Equations60 Questions
Exam 10: Parametric Equations and Polar Coordinates60 Questions
Exam 11: Infinite Sequences and Series60 Questions
Exam 12: Vectors and the Geometry of Space54 Questions
Exam 13: Vector Functions58 Questions
Exam 14: Partial Derivatives39 Questions
Exam 15: Multiple Integrals60 Questions
Exam 16: Vector Calculus59 Questions
Exam 17: Second-Order Differential Equations60 Questions
Select questions type
Suppose the distance (in feet) covered by a car moving along a straight road after sec is given by the function . Calculate the (instantaneous) velocity of the car when .
(Multiple Choice)
4.8/5  (34)
(34)
The following figure shows a portion of the graph of a function defined on the interval . Sketch the complete graph of if it is known is odd.
![The following figure shows a portion of the graph of a function f defined on the interval [ - 1,1 ] . Sketch the complete graph of f if it is known f is odd.](https://storage.examlex.com/TB8681/11ecdf2d_e824_c9f2_b402_3f4a3b37536a_TB8681_11.jpg)
(Essay)
4.9/5  (31)
(31)
The displacement (in feet) of a certain particle moving in a straight line is given by
where is measured in seconds. Find the average velocity over the interval .
Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (42)
(42)
The graphs of and are given.
a) For what values of is ?
b) Find the values of and .
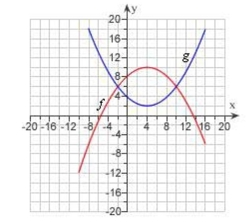
(Short Answer)
4.9/5  (29)
(29)
For what value of the constant is the function continuous on
Select the correct answer.
(Multiple Choice)
4.7/5  (26)
(26)
If a rock is thrown upward on the planet Mars with a velocity of , its height in meters seconds later is given by
Find the average velocity over the time interval .
(Multiple Choice)
4.8/5  (30)
(30)
The position of a car is given by the values in the following table. t (seconds) 0 1 2 3 4 s (meters) 0 21.9 25.8 69.2 92.2
Find the average velocity for the time period beginning when and lasting 2 seconds.
(Multiple Choice)
4.9/5  (33)
(33)
Find the numbers, if any, where the function is discontinuous.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)