Exam 6: Applications of Integration
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the volume of the solid obtained by rotating about the axis the region bounded by the curves.
(Short Answer)
4.8/5  (32)
(32)
A painting in an art gallery has height and is hung so that lower edge is a distance above the eye of an observer (as in the figure). How far from the wall should the observer stand to get the best view? (In other words, where should the observer stand so as to maximize the angle subtended at his eye by the painting?) Select the correct answer.
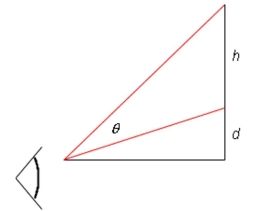
(Multiple Choice)
4.9/5  (38)
(38)
Determine from the table.
The values from the table are given to the nearest ten thousandth. Select the correct answer.
x f(x) -1 20.0855 0 1 1 0.0498 2 0.0025
(Multiple Choice)
4.9/5  (34)
(34)
Calculate , where . State the domain and range of . Calculate .
(Short Answer)
4.8/5  (36)
(36)
Use Newton's method to find the roots of the equation correct to five decimal places.
(Short Answer)
4.7/5  (30)
(30)
Find an equation of the tangent line to the curve at the given point.
(Short Answer)
4.9/5  (41)
(41)
Find the inverse of . Then sketch the graphs of and on the same set of axes.
(Short Answer)
4.9/5  (42)
(42)
Showing 61 - 80 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)