Exam 7: Techniques of Integration
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
The region is represented below.
Find the area of this region to two decimal places. Select the correct answer.
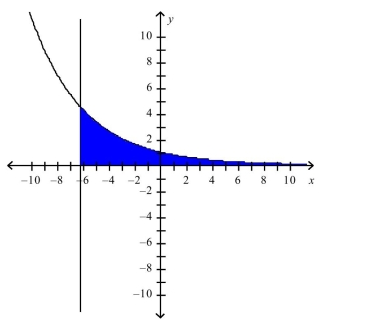
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether the integral converges or diverges. If it converges, find its value.
(Short Answer)
4.8/5  (29)
(29)
Use long division to evaluate the integral.
The choices are rounded to 3 decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Evaluate the integral using the indicated trigonometric substitution.
(Multiple Choice)
4.8/5  (36)
(36)
A manufacturer of light bulbs wants to produce bulbs that last about 700 hours but, of course, some bulbs burn out faster than others. Let be the fraction of the company's bulbs that burn out before hours. lies between 0 and 1 .
Let . What is the value of ?
(Short Answer)
5.0/5  (38)
(38)
Use Simpson's Rule to approximate the integral with answers rounded to four decimal places.
(Multiple Choice)
4.9/5  (39)
(39)
Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with subintervals.
(Short Answer)
4.9/5  (34)
(34)
Showing 121 - 140 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)