Exam 7: Techniques of Integration
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Use the Table of Integrals to evaluate the integral to three decimal places.
(Short Answer)
4.7/5  (40)
(40)
Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with subintervals.
(Short Answer)
4.9/5  (36)
(36)
Find the integral using an appropriate trigonometric substitution.
(Short Answer)
4.7/5  (38)
(38)
Evaluate the integral using integration by parts with the indicated choices of and .
(Multiple Choice)
4.8/5  (42)
(42)
Determine whether the improper integral converges or diverges, and if it converges, find its value.
(Multiple Choice)
4.8/5  (40)
(40)
Determine whether the improper integral converges or diverges, and if it converges, find its value.
(Short Answer)
4.9/5  (38)
(38)
The region is represented below. Find the area of this region to two decimal places.
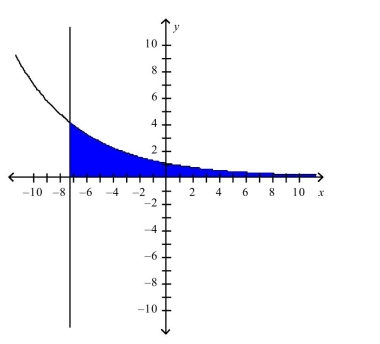
(Short Answer)
4.9/5  (39)
(39)
Showing 61 - 80 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)