Exam 9: Differential Equations
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the solution of the differential equation that satisfies the initial condition .
(Short Answer)
4.9/5  (36)
(36)
Use Euler's method with step size to estimate , where is the solution of the initial-value problem. Round your answer to four decimal places.
(Short Answer)
4.8/5  (38)
(38)
Kirchhoff's Law gives us the derivative equation .
If , use Euler's method with step size to estimate after second.
(Short Answer)
4.9/5  (38)
(38)
Let be the performance level of someone learning a skill as a function of the training time . The graph of is called a learning curve. We propose the differential equation
as a reasonable model for learning, where is a positive constant. Solve it as a linear differential equation.
(Short Answer)
4.8/5  (36)
(36)
Use Euler's method with step size to estimate , where is the solution of the initial-value problem. Round your answer to four decimal places. Select the correct answer.
(Multiple Choice)
4.9/5  (43)
(43)
Solve the differential equation. Select the correct answer.
(Multiple Choice)
4.8/5  (37)
(37)
A phase trajectory is shown for populations of rabbits and foxes . Describe how each population changes as time goes by. Select the correct answer.
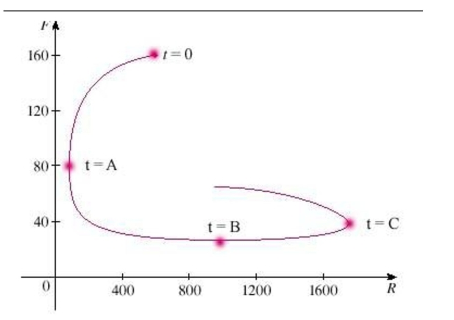 Select the correct statement.
Select the correct statement.
(Multiple Choice)
4.9/5  (36)
(36)
A tank contains of brine with of dissolved salt. Pure water enters the tank at a rate of . The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank after 20 minutes?
(Short Answer)
4.9/5  (36)
(36)
A curve passes through the point and has the property that the slope of the curve at every point is 3 times the -coordinate . What is the equation of the curve?
(Short Answer)
4.8/5  (26)
(26)
A common inhabitant of human intestines is the bacterium Escherichia coli. A cell of this bacterium in a nutrient-broth medium divides into two cells every 20 minutes. The initial population of a culture is 50 cells. Find the number of cells after 6 hours.
(Multiple Choice)
4.7/5  (27)
(27)
A sum of is invested at interest. If is the amount of the investment at time for the case of continuous compounding, write a differential equation and an initial condition satisfied by .
(Short Answer)
4.9/5  (40)
(40)
Solve the initial-value problem. Select the correct answer.
(Multiple Choice)
5.0/5  (40)
(40)
Showing 41 - 60 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)