Exam 9: Differential Equations
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Let be a positive number. A differential equation of the form
where is a positive constant is called a doomsday equation because the exponent in the expression is larger than the exponent 1 for natural growth. An especially prolific breed of rabbits has the growth term . If 3 such rabbits breed initially and the warren has 28 rabbits after 5 months, then when is doomsday?
(Short Answer)
4.8/5  (33)
(33)
A curve passes through the point and has the property that the slope of the curve at every point is 4 times the -coordinate . What is the equation of the curve?
(Multiple Choice)
4.9/5  (31)
(31)
A population is modeled by the differential equation.
For what values of is the population increasing? Select the correct answer
(Multiple Choice)
4.8/5  (37)
(37)
Suppose that a population grows according to a logistic model with carrying capacity 7,000 and per year. Choose the logistic differential equation for these data.
(Multiple Choice)
4.9/5  (43)
(43)
In the circuit shown in Figure, a generator supplies a voltage of volts, the inductance is , the resistance is , and . Find the current after the switch is closed. Round your answer to two decimal places.
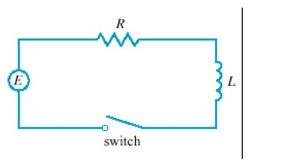
(Short Answer)
4.9/5  (25)
(25)
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people. In an isolated town of 6,000 inhabitants, 160 people have a disease at the beginning of the week and 1,500 have it at the end of the week. How long does it take for of the population to be infected?
(Short Answer)
4.9/5  (31)
(31)
A population is modeled by the differential equation
For what values of is the population decreasing?
(Short Answer)
5.0/5  (40)
(40)
The population of the world was about billion in 1990 . Birth rates in the 1990 s range from 35 to 40 million per year and death rates range from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 100 billion. Use the logistic model to predict the world population in the 2,450 year. Calculate your answer in billions to one decimal place. (Because the initial population is small compared to the carrying capacity, you can take to be an estimate of the initial relative growth rate.)
(Multiple Choice)
4.8/5  (42)
(42)
Select a direction field for the differential equation from a set of direction fields labeled I-IV.
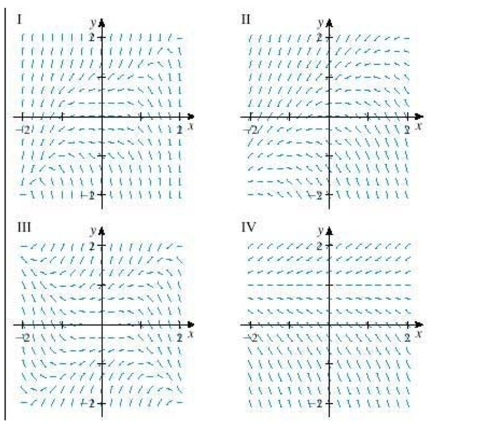
(Short Answer)
4.9/5  (45)
(45)
A function satisfies the differential equation .
What are the constant solutions of the equation?
(Short Answer)
4.9/5  (33)
(33)
Suppose that a population develops according to the logistic equation
where is measured in weeks. What is the carrying capacity?
Select the correct answer.
(Multiple Choice)
4.8/5  (41)
(41)
Consider the differential equation
as a model for a fish population, where is measured in weeks and is a constant. For what values of does the fish population always die out?
(Short Answer)
4.8/5  (44)
(44)
Choose the differential equation corresponding to this direction field.t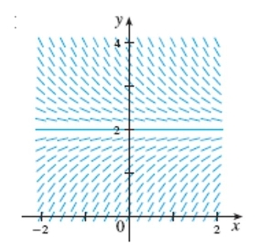
(Multiple Choice)
4.9/5  (39)
(39)
We modeled populations of aphids and ladybugs with a Lotka-Volterra system. Suppose we modify those equations as follows:
Find the equilibrium solution.
(Short Answer)
4.8/5  (41)
(41)
Showing 81 - 100 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)