Exam 6: Random Variables and Probability Distributions

$\text { If random variables } x _ { 1 } \text { and } x _ { 2 } \text { are independent, then } \sigma _ { x _ { 1 } + x _ { 2 } } ^ { 2 } = \sigma _ { x _ { 1 } } ^ { 2 } + \sigma _ { x _ { 2 } } ^ { 2 }$

(True/False)

4.8/5

(38)

Question 21

The density curve for a continuous random variable is shown below. Use this curve to find the following probabilities: $The density curve for a continuous random variable is shown below. Use this curve to find the following probabilities: 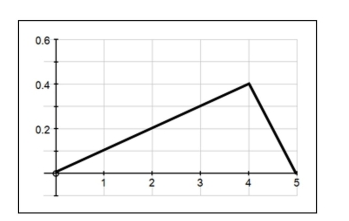a) P ( x < 1 ) b) P ( 2 < x < 4 ) You may need to use the following area formulas in your calculations: Area of a rectangle: A = l w Area of a trapezoid: A = \frac { 1 } { 2 } h \left( b _ { 1 } + b _ { 2 } \right) Area of a right triangle: A = \frac { 1 } { 2 } a b$ a) $P ( x < 1 )$ b) P ( 2 < x < 4 ) You may need to use the following area formulas in your calculations: Area of a rectangle: $A = l w$ Area of a trapezoid: $A = \frac { 1 } { 2 } h \left( b _ { 1 } + b _ { 2 } \right)$ Area of a right triangle: $A = \frac { 1 } { 2 } a b$

(Short Answer)

4.8/5

(42)

Question 22

$\text { For random variables } x \text { and } y \text {, if } y = a + b x \text {, then } \sigma _ { y } = a + b \sigma _ { x }$

(True/False)

4.8/5

(28)

Question 23

Each course at a large university has either a final exam or a final paper. The table below presents the distribution of the number of final exams that students at the university take in the Fall term, and their associated probabilities. What is the mean of this distribution? 1 2 3 ( )

(Essay)

4.7/5

(28)

Question 24

Let z denote a random variable having a standard normal distribution. Determine each of the following probabilities. a) $P ( z < 1.28 )$ b) $P ( z < - 1.05 )$ c) $P ( z > - 2.51 )$ d) $P ( - 1.30 < z < 1.54 )$

(Essay)

4.7/5

(34)

Question 25

What is a random variable?

(Short Answer)

4.7/5

(30)

Question 26

What is a random variable?

(Short Answer)

4.8/5

(31)

Question 27

A gasoline tank for a certain model car is designed to hold 12 gallons of gas. Suppose that the actual capacity of gas tanks in cars of this type is well approximated by a normal distribution with mean 12.0 gallons and standard deviation 0.2 gallons. What is the approximate probability that a randomly selected car of this model will have a gas tank that holds at most 11.7 gallons?

(Essay)

4.8/5

(33)

Question 28

What information about a probability distribution do the mean and standard deviation of a random variable provide?

(Essay)

4.7/5

(39)

Question 29

For a variable z that has a standard normal distribution, a) What is the probability that $z < - 2.45$ ? b) What is the probability that $z < + 1.67$ ? c) What is the probability that $\mathrm { z }$ is between $- 1.43$ and $+ 1.43$ d) What value of $z$ separates the smaller $10 \%$ of the standard normal distribution from the larger $90 \%$ ? e) What values of $- z$ and $+ z$ separate the middle $95 \%$ of the standard normal distribution from the extreme $5 \%$ ?

(Essay)

4.9/5

(41)

Question 30

The Economist is a weekly newspaper that focuses on international politics, business news, and opinion. Each year the "Big Mac Index," the price (\ U. S.) of a Big Mac in countries around the world, is published as a light-hearted way of comparing currencies. Displayed at right are 3 views of the BMIs in mid-summer, 2007: the normal probability plot, a box and whisker plot, and a histogram. Using one of the three plots, discuss any indication of skew you see. In your discussion be specific about what aspect(s) of the graph you feel is/are indicative of skew. $\begin{array} { l } \text { The Economist is a weekly newspaper } \\ \text { that focuses on international politics, } \\ \text { business news, and opinion. Each } \\ \text { year the Big Mac Index, the price (\$ } \\ \text { U. S.) of a Big Mac in countries } \\ \text { around the world, is published as a } \\ \text { light-hearted way of comparing } \\ \text { currencies. Displayed at right are 3 } \\ \text { views of the BMIs in mid-summer, } \\ \text { 2007: the normal probability plot, a } \\ \text { box and whisker plot, and a } \\ \text { histogram. } \\ \text { Using one of the three plots, discuss } \\ \text { any indication of skew you see. In } \\ \text { your discussion be specific about } \\ \text { what aspect(s) of the graph you feel } \\ \text { is/are indicative of skew. } \end{array}$

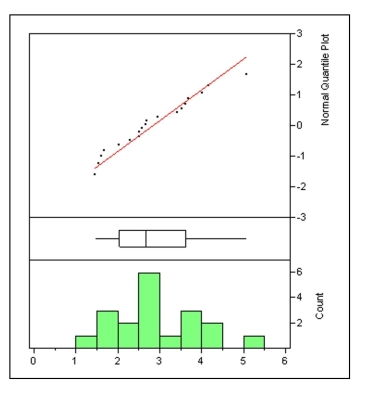
(Essay)

4.9/5

(31)

Question 31

Determine the following areas under the standard normal (z) curve. a) The area under the z curve to the left of 1.56 b) The area under the z curve to the left of -2.13 c) The area under the z curve to the right of 0.88 d) The area under the z curve to the right of -1.23 e) The area under the z curve between -2 and 3 f) The area under the z curve between -2.4 and -1.4

(Essay)

4.8/5

(32)

Question 32

Electric power cords are a common hazard in households with computers. They are easily tripped over and the delicate computer equipment may be pulled from tables and damaged. A new "breakaway" power cord has been designed by Alpha Enterprises. Alpha has determined that a breakaway force of between 3.0 and 5.0 pounds is appropriate. (If the force is too low the cord would break in normal use; if the force is too high the cord would not be effective.) Alpha can order cord material from two companies, Beta and Gamma. The breakaway force for the Beta material is approximately normally distributed with a mean of 4.5 pounds and a standard deviation of 1.0 pounds. The breakaway force for the Gamma material is approximately normally distributed with a mean of 4.0 pounds and a standard deviation of 1.5 pounds. Alpha will choose the cord material that has the higher probability of breaking within the specified 3.0 and 5.0 pound limits. From which company should Alpha order cord material? Provide appropriate statistical justification for your choice.

(Essay)

4.7/5

(27)

Question 33

Road construction in the town of Hiawatha has presented some problems for the traffic engineers. Small businesses such as Bev's Hair Gallery will require an alternate entrance for their customers. This will in turn create a minor congestion of traffic nearby because cars will be backed up and the entrance to the parking lot. The engineers have studied the problem using simulations based on current traffic patterns. The results from 500 trials are shown below: Number of times cars are backed up at the entrance 0 250 1 150 2 75 3 25 Let the random variable k = number of cars backed up at the entrance. a) Fill in the table below with the estimated probability distribution of k, and sketch a probability histogram for x. Probability distribution k (x) 2 3 Probability histogram $Road construction in the town of Hiawatha has presented some problems for the traffic engineers. Small businesses such as Bev's Hair Gallery will require an alternate entrance for their customers. This will in turn create a minor congestion of traffic nearby because cars will be backed up and the entrance to the parking lot. The engineers have studied the problem using simulations based on current traffic patterns. The results from 500 trials are shown below: \begin{array} { | c | c | } \hline \boldsymbol { k } & \begin{array} { l } \text { Number of times } \boldsymbol { k } \\ \text { cars are backed up } \\ \text { at the entrance } \end{array} \\ \hline 0 & 250 \\ 1 & 150 \\ 2 & 75 \\ 3 & 25 \\ \hline \end{array} Let the random variable k = number of cars backed up at the entrance. a) Fill in the table below with the estimated probability distribution of k, and sketch a probability histogram for x. Probability distribution \begin{array}{|l|l|} \hline k & \mathrm{P}(x) \\ \hline \mathbf{0} & \\ \hline \mathbf{1} & \\ \hline 2 & \\ \hline 3 & \\ \hline \end{array} Probability histogram 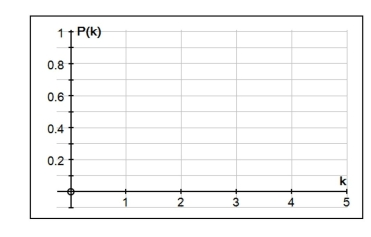b) Using the estimated probabilities in part (a), calculate the following: i) P ( k = 1 ) , the probability that 1 car is backed up at the entrance. ii) P ( x < 2 ) , the probability that fewer than 2 cars are backed up at the entrance iii) P ( x \geq 1 ) , the probability that at least 1 car is backed up at the entrance$ b) Using the estimated probabilities in part (a), calculate the following: i) $P ( k = 1 )$ , the probability that 1 car is backed up at the entrance. ii) $P ( x < 2 )$ , the probability that fewer than 2 cars are backed up at the entrance iii) $P ( x \geq 1 )$ , the probability that at least 1 car is backed up at the entrance

(Essay)

4.8/5

(33)

Question 34

$\text { For a discrete random variable } x , \mu _ { x } = \sum _ { x \text { values } } x \cdot p ( x )$

(True/False)

4.9/5

(30)

Question 35

When driving the nation's highways, Anna is known as something of a lead foot. Her number of miles per hour over the speed limit varies, but has a mean of 7.5 mph and standard deviation of 2 mph. Unfortunately her state adjusts the fines so that the amount of the fine (in dollars) is given by the formula: $F = 10 ( \text { MilesOver } ) + 112$ where F is the amount of the fine, and MilesOver is the number of miles over the speed limit. Let random variable F be the amount of her fine if she is stopped for speeding. a) What is the mean of F? b) What is the standard deviation of F?

(Essay)

4.7/5

(38)

Question 36

Inspecting meat is a very important part of the process of ensuring healthy food. So that meat inspectors do not fall into a pattern of inspection, they use a 4-sided die to decide whether or not to sample the meat from a particular "side" of beef. The meat inspector rolls the die and if it comes up a 4, a sample is taken of that meat. Define random variable x number of samples inspected in a meat locker with 30 sides of beef. a) What is the mean of the random variable x? b) What is the standard deviation of the random variable x?

(Essay)

4.9/5

(26)

Question 37

In a study performed by the statistics classes at Jefferson High School, city parking spaces were examined for compliance with the requirement to put money in the parking meters. Overall, the students found that 80% of metered parking places had meters that were not expired, and 20% had meters that were expired. If the traffic officer in charge of ticketing checks meters at random, what is the probability he or she will find an expired meter before the 3rd one checked?

(Essay)

4.8/5

(37)

Question 38

Using the notation C = continuous and D = discrete, indicate whether each of the random variables is discrete or continuous. a) The number of steps to the principal's office from a randomly selected location at a particular school. b) The average night time temperature on a randomly selected day in July at Long's Peak in Colorado c) The number of eggs in a kitchen on a randomly selected day. d) The number of sentences in a short story selected at random from a collection of short stories. e) The circumference of a randomly selected California redwood tree

(Essay)

4.8/5

(37)

Question 39

The graphs below are normal probability plots of the vocabulary and math concept scores on a standardized exam for a large sample of students. One of the score distributions is approximately normal. Identify the score distribution that is approximately normal and explain the reason for your choice.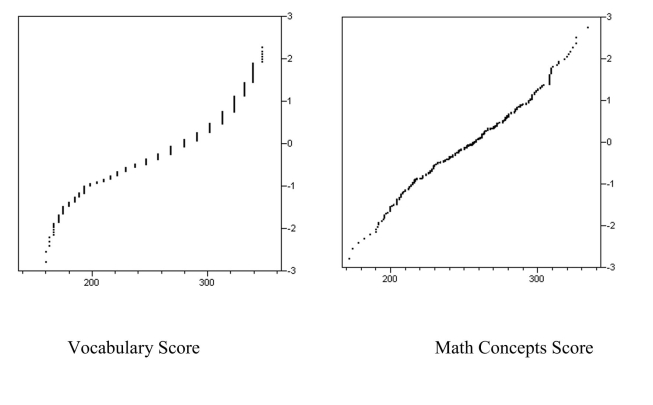

(Essay)

4.7/5

(31)

Question 40

Showing 21 - 40 of 57

$\text { If random variables } x _ { 1 } \text { and } x _ { 2 } \text { are independent, then } \sigma _ { x _ { 1 } + x _ { 2 } } ^ { 2 } = \sigma _ { x _ { 1 } } ^ { 2 } + \sigma _ { x _ { 2 } } ^ { 2 }$

$\text { For random variables } x \text { and } y \text {, if } y = a + b x \text {, then } \sigma _ { y } = a + b \sigma _ { x }$

Each course at a large university has either a final exam or a final paper. The table below presents the distribution of the number of final exams that students at the university take in the Fall term, and their associated probabilities. What is the mean of this distribution? 1 2 3 ( )

Let z denote a random variable having a standard normal distribution. Determine each of the following probabilities. a) $P ( z < 1.28 )$ b) $P ( z < - 1.05 )$ c) $P ( z > - 2.51 )$ d) $P ( - 1.30 < z < 1.54 )$

What is a random variable?

What is a random variable?

What information about a probability distribution do the mean and standard deviation of a random variable provide?

$\text { For a discrete random variable } x , \mu _ { x } = \sum _ { x \text { values } } x \cdot p ( x )$

The graphs below are normal probability plots of the vocabulary and math concept scores on a standardized exam for a large sample of students. One of the score distributions is approximately normal. Identify the score distribution that is approximately normal and explain the reason for your choice.

Collecting Data in Reasonable Ways

Graphical Methods for Describing Data Distributions

Numerical Methods for Describing Data Distributions

Describing Bivariate Numerical Data

Probability

Selecting an Appropriate Method

Sampling Variability Sampling

Estimation Using a Single Sample

Asking and Answering Questions About a Population Proportion

Asking and Answering Questions About the Difference Between Two Population Proportions

Asking and Answering Questions About a Population Mean

Asking and Answering Questions About the Difference Between Two Means

Learning From Experiment Data

Filters

Exam 6: Random Variables and Probability Distributions

For random variables x and y, if y=a+bx, then σy=a+bσx\text { For random variables } x \text { and } y \text {, if } y = a + b x \text {, then } \sigma _ { y } = a + b \sigma _ { x } For random variables x and y, if y=a+bx, then σy​=a+bσx​

Each course at a large university has either a final exam or a final paper. The table below presents the distribution of the number of final exams that students at the university take in the Fall term, and their associated probabilities. What is the mean of this distribution? 1 2 3 ( )

What is a random variable?

What is a random variable?

What information about a probability distribution do the mean and standard deviation of a random variable provide?

For a discrete random variable x,μx=∑x values x⋅p(x)\text { For a discrete random variable } x , \mu _ { x } = \sum _ { x \text { values } } x \cdot p ( x ) For a discrete random variable x,μx​=∑x values ​x⋅p(x)

The graphs below are normal probability plots of the vocabulary and math concept scores on a standardized exam for a large sample of students. One of the score distributions is approximately normal. Identify the score distribution that is approximately normal and explain the reason for your choice.

Collecting Data in Reasonable Ways

Graphical Methods for Describing Data Distributions

Numerical Methods for Describing Data Distributions

Describing Bivariate Numerical Data

Probability

Selecting an Appropriate Method

Sampling Variability Sampling

Estimation Using a Single Sample

Asking and Answering Questions About a Population Proportion

Asking and Answering Questions About the Difference Between Two Population Proportions

Asking and Answering Questions About a Population Mean

Asking and Answering Questions About the Difference Between Two Means

Learning From Experiment Data

Filters

$\text { For random variables } x \text { and } y \text {, if } y = a + b x \text {, then } \sigma _ { y } = a + b \sigma _ { x }$

$\text { For a discrete random variable } x , \mu _ { x } = \sum _ { x \text { values } } x \cdot p ( x )$