Exam 6: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Find which of the following system of inequalities has a right triangle as a graphed solution set. System I: System II: System III:
(Multiple Choice)
4.9/5  (34)
(34)
An investor has $750,000 to invest in two types of investments. Type A pays 4% annually and type B pays 5% annually. To have a well-balanced portfolio, the investor imposes the following conditions. At least one-third of the total portfolio is to be allocated to type A investments and at least one-third of the portfolio is to be allocated to type B investments. What is the optimal amount that should be invested in each investment? 
(Multiple Choice)
4.8/5  (37)
(37)
Find the minimum and maximum values of the objective function and where they occur, subject to the constraints . 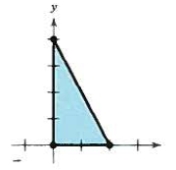
(Multiple Choice)
4.9/5  (33)
(33)
For the given supply and demand equations, find the consumer surplus. Round to the nearest dollar. Demand Supply
P = 160 - 0.00006x p = 110 + 0.00003x
(Multiple Choice)
4.9/5  (28)
(28)
Sketch the graph of the solution set of each system of inequalities.
(Multiple Choice)
4.8/5  (39)
(39)
An accounting firm charges $2500 for an audit and $350 for a tax return. Research and available resources have indicated the following constraints. The firm has 900 hours of staff time available each week.
The firm has 155 hours of review time available each week.
Each audit requires 75 hours of staff time and 10 hours of review time.
Each tax return requires 12.5 hours of staff time and 2.5 hours of review time.
What numbers of audits and tax returns will bring in an optimal revenue?
(Multiple Choice)
4.8/5  (29)
(29)
A total of $50,000 is invested in two funds paying 8% and 13% simple interest. The total yearly interest is $5100. How much is invested at the 8% rate?
(Multiple Choice)
4.9/5  (42)
(42)
Which of the following vertices of the constraint region shown is a maximum value of the objective function below. 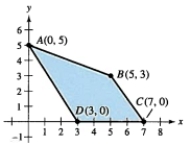
(Multiple Choice)
4.8/5  (36)
(36)
Which of the following vertices of the constraint region shown is a minimum value of the objective function below. 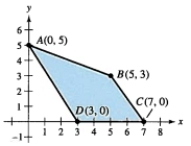
(Multiple Choice)
4.7/5  (40)
(40)
Use back-substitution to solve the system of linear equations.
(Multiple Choice)
4.8/5  (24)
(24)
You are offered two different jobs. Company A offers an annual salary of $32,500 plus a year-end bonus of 2.5% of your total sales. Company B offers a salary of $28,000 plus a year-end bonus of 5.5% of your total sales. What is the amount you must sell in one year to earn the same salary working for either company?
(Multiple Choice)
4.7/5  (37)
(37)
Sketch the graph of the solution set of each system of inequalities.
(Multiple Choice)
4.8/5  (38)
(38)
A company makes two types of telephone answering machines: the standard model and the deluxe model. Each machine passes through three processes: and One standard answering machine requires 1 hour in 4 hours in and 3 hours in One deluxe answering machine requires 3 hours in 5 hours in and 1 hour in Because of employee work schedules, is available for 24 hours, is available for 47 hours, and is available for 27 hours. If the profit is $22 for each standard model and $23 for each deluxe model, how many units of each type should the company produce to maximize profit?
(Multiple Choice)
4.8/5  (30)
(30)
An ice cream supplier has two machines that produce vanilla and chocolate ice cream. To meet one of its contractual obligations, the company must produce at least 9 gallons of vanilla ice cream and 15 gallons of chocolate ice cream per day. One machine makes 6 gallons of vanilla and 3 gallons of chocolate ice cream per hour. The second machine makes 1 gallons of vanilla and 4 gallons of chocolate ice cream per hour. It costs $28 per hour to run machine 1 and $22 per hour to run machine 2. How many hours should each machine be operated to fulfill the contract at the least expense?
(Multiple Choice)
4.8/5  (40)
(40)
Showing 61 - 80 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)