Exam 6: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Solve the system below by method of substitution, if possible.
(Multiple Choice)
4.7/5  (34)
(34)
A manufacturer produces two models of bicycles. The times (in hours) required for assembling, painting, and packaging each model are shown in the table. Process Model A Model B Assembling 2 2.5 Painting 4 1 Packaging 1 0.75 The total times available for assembling, painting, and packing are 4000 hours, 4800 hours, and 1500 hours, respectively. The profit per unit are $50 for model A and $75 for model B. What is the optimal production level for each model? What is the optimal profit?
(Multiple Choice)
4.9/5  (38)
(38)
Which of the following systems of equations has as a solution the ordered triple System I: System II: System III:
(Multiple Choice)
4.9/5  (42)
(42)
Which of the following three ordered triples are of the given form below. Triple I :
Triple II :
Triple III :
(Multiple Choice)
4.9/5  (36)
(36)
An airplane flying into a headwind travels 328 miles in 2 hours and 44 minutes. On the return flight, the distance is traveled in 2 hours. Find the airspeed of the plane and the speed of the wind, assuming that both remain constant.
(Multiple Choice)
4.9/5  (35)
(35)
A mixture of 6 gallons of chemical A, 7 gallons of chemical B, and 10 gallons of chemical C is required to kill a crop destroying insect. Commercial spray X contains 1, 2, and 3 parts of these chemicals, respectively. Commercial spray Y contains only chemical C. Commercial spray Z contains chemicals A, B, and C in equal amounts. How much of commercial spray is needed to obtain the desired mixture?
(Multiple Choice)
5.0/5  (36)
(36)
One acetic acid solution is 80% water and another is 45% water. How many liters of each solution should be mixed to produce 10 liters of a solution that is 73% water?
(Multiple Choice)
4.8/5  (32)
(32)
Find an objective function that has a minimum value at the indicated vertex D of the constraint region shown below. 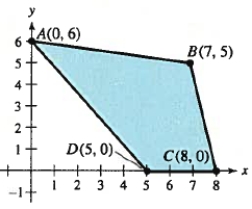
(Multiple Choice)
4.8/5  (35)
(35)
Find an equation of the form whose graph passes through the points and
(Multiple Choice)
4.9/5  (38)
(38)
The supply and demand equations for a small LCD television are given by where is the price (in dollars) and represents the number of televisions. For how many units will the quantity demanded equal the quantity supplied? What price corresponds to this value?
(Multiple Choice)
4.7/5  (35)
(35)
Find the consumer surplus for the pair of demand and supply equations below. p=75-0.00002x Demand p=30+0.00003x Suppply
(Multiple Choice)
4.8/5  (31)
(31)
Use the statements below to write a system of equations. Solve the system by elimination. The sum of twice a number and a number is 4. The difference of and is 11.
(Multiple Choice)
4.9/5  (30)
(30)
Determine which of the following systems of equations is in row-echelon form. System I: System II: System III:
(Multiple Choice)
4.8/5  (39)
(39)
Find the equilibrium point of the demand and supply equations. (The equilibrium point is the price p and number of units x that satisfy both the demand and supply equations.) Demand Supply
(Multiple Choice)
4.7/5  (40)
(40)
Showing 81 - 96 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)