Exam 6: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Find an objective function that has a minimum value at the indicated vertices A and D of the constraint region shown below. 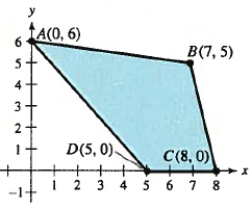
(Multiple Choice)
4.8/5  (40)
(40)
A farming cooperative mixes two brands of cattle feed. Brand X costs $30 per bag, and brand Y costs $25 per bag. Research and available resources have indicated the following constraints. Brand X contains two units nutritional element A, two units of element B, and two units of element C.
Brand Y contains one unit of nutritional element A, nine units of element B, and three units of element C.
The minimum requirements for nutrients A, B, and C are 12 units, 36 units, and 24 units, respectively.
What is the optimal number of bags of each brand that should be mixed? What is optimal cost?
(Multiple Choice)
4.7/5  (33)
(33)
A company makes two models of doghouses. The times (in hours) required for assembling, painting, and packaging are shown in the table. Process Model A Model B Assembling 2.5 3 Painting 2 1 Packaging 0.75 1.25 The total times available for assembling, Painting, and packaging are 4000 hours, 2500 hours, and 1500 hours, respectively. The profits per unit are $60 for model A and $75 for model B. what is the optimal production level for each model? What is the optimal profit?
(Multiple Choice)
4.9/5  (39)
(39)
Solve the system below by elimination if possible. Then state whether the system below is consistent or inconsistent.
(Multiple Choice)
4.7/5  (36)
(36)
Find the maximum value of the objective function and where it occurs, subject to the indicated constraints. (You should graph the feasible solutions on the grid below before you attempt to find the minimum and maximum values.) Objective function: Constraints: 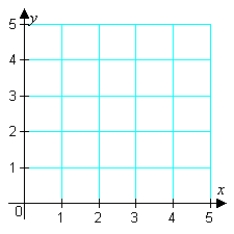
(Multiple Choice)
4.9/5  (43)
(43)
Find the least squares regression line y = ax + b for the points by solving the system for a and b. nb+ a= b+ a= Points: space
(Multiple Choice)
4.9/5  (40)
(40)
Find the minimum and maximum values of the objective function and where they occur, subject to the indicated constraints. Objective function: Constraints: 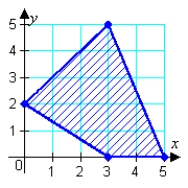
(Multiple Choice)
4.9/5  (31)
(31)
Find the equation of the circle that passes through the points .
(Multiple Choice)
4.8/5  (33)
(33)
Derive a set of inequalities to describe the region. Triangle: vertices at (0, 0), (3, 0), (3, 5)
(Multiple Choice)
4.9/5  (27)
(27)
A real estate company borrows $700,000. Some of the money is borrowed at 5%, some at 9%, and some at 11% simple annual interest. How much is borrowed at the 5% rate when the total annual interest is $55,000 and the amount borrowed at 9% is the same as the amount borrowed at 11%?
(Multiple Choice)
4.9/5  (40)
(40)
Use a graphing utility to find the point(s) of intersection of the graphs.
(Multiple Choice)
4.9/5  (42)
(42)
The costs to a store two models of Global Positioning System (GPS) receivers are $80 and $100. The $80 model yields a profit of $25 and the $100 model yields a profit of $30. Market tests and available resources indicate the following constraints. The merchant estimates that the total monthly demand will not be exceed 200 units.
The merchant does not want to invest more than $18,000 in GPS receiver inventory.
What is the optimal inventory level for each model what is optimal profit?
(Multiple Choice)
4.9/5  (38)
(38)
A furniture company produces tables and chairs. Each table requires 2.5 hours in the assembly center and 1.75 hours in the finishing center. Each chair requires 1 hour in the assembly center and 1.25 hours in the finishing center. The company's assembly center is available 16 hours per day, and its finishing center is available 12 hours per day. Let and be the number of tables and chairs produced per day, respectively. Find a system of inequalities describing all possible production levels.
(Multiple Choice)
4.9/5  (26)
(26)
The sales of various types of lawn and garden items vary according to the season. At a certain home improvement store, the monthly sales H of garden hoses (hoses sold per month) declines from July to October whereas the monthly sales of lawn rakes R (rakes sold per month) increase during this same interval. The sales of these two items during the calendar months July-October are modeled by the equations: H(t) = 64 - 6t
R(t) = 17t - 97,
Where t is the month (t = 7 corresponds to July). In which month does the number of rakes sold equal the number of hoses sold?
(Multiple Choice)
4.7/5  (30)
(30)
Showing 41 - 60 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)