Exam 5: Exponential and Logarithmic Functions
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Use algebraic procedures to find the exact solution of the equation .
(Multiple Choice)
4.9/5  (35)
(35)
Use a calculator to evaluate the function for the given value of , . Round your result to three decimal places.
(Multiple Choice)
4.8/5  (42)
(42)
Evaluate the expression below. Round your results to three decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the exponential equation algebraically. Approximate the result to three decimal places.
(Multiple Choice)
4.9/5  (21)
(21)
A stock analyst attempts to express the price p of a share of XYZ stock as an exponentially increasing function of the time since XYZ's initial public offering (IPO): , where m is the number of months since the IPO. The price of a share was $10.00 at the time of the IPO and $12.80 four months after the IPO. What is the approximate value of k? Round to the nearest thousandth.
(Multiple Choice)
4.8/5  (41)
(41)
The average monthly sales (in billions of dollars) in retail trade in the United States from 1996 to 2005 can be approximated by the model where represents the year, with corresponding to 1996. Estimate the year in which the average monthly sales first exceeded $310 billion.
(Multiple Choice)
4.8/5  (40)
(40)
The decibel (dB) is defined as , where P2 is the power of a particular signal and P1 is the power of some reference signal. In the case of sounds, the reference signal is a sound level that is just barely audible. How many dBs does a sound have if its power is 7,320,000 times that of the reference sound? Round to the nearest tenth.
(Multiple Choice)
4.8/5  (31)
(31)
Use a calculator to evaluate . Round your result to three decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
The number of certain type of bacteria increases according to the model where t is time (in hours)
a)Find P(0).
b)Find P(5).
c)Find P(10).
d)Find P(24).
(Multiple Choice)
4.9/5  (26)
(26)
Evaluate the logarithm using the change of base formula. Round to 3 decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
An investment is expected to pay 7% per year compounded continuously. If you want the value of the investment to be $600,000 after 25 years, how much should you invest initially? Round to the nearest dollar.
(Multiple Choice)
4.8/5  (28)
(28)
Determine whether the function has an inverse function, If it does, find its inverse function.
(Multiple Choice)
4.9/5  (35)
(35)
Write the expression below as a single logarithm with a coefficient of 1. Assume all variable expressions represent positive real numbers.
(Multiple Choice)
4.7/5  (29)
(29)
Match the function below with its graph. Graph I : 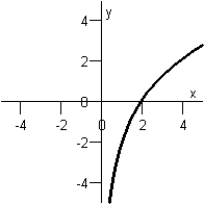 Graph IV:
Graph IV: 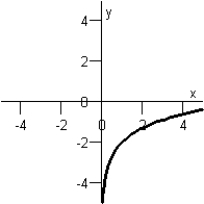 Graph II:
Graph II: 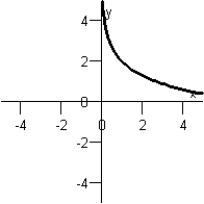 Graph V:
Graph V: 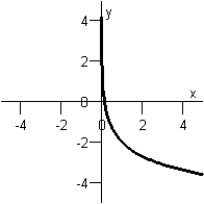 Graph III:
Graph III: 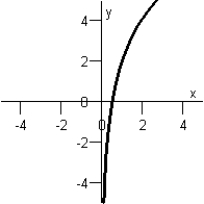
(Multiple Choice)
4.9/5  (37)
(37)
Showing 61 - 80 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)