Exam 6: The Normal Distributions and Other Continuous Distributions

The amount of time necessary for assembly line workers to complete a product is a normal variable with a mean of 15 minutes and a standard deviation of 2 minutes.The probability is __________ that a product is assembled in more than 19 minutes.

You were told that the mean score on a statistics exam is 75 with the scores normally distributed.In addition, you know the probability of a score between 55 and 60 is 4.41% and that the probability of a score greater than 90 is 6.68%.What is the probability of a score between 60 and 75?

Theoretically, the mean, median, and the mode are all equal for a normal distribution.

SCENARIO 6-3 Suppose the time interval between two consecutive defective light bulbs from a production line has a uniform distribution over an interval from 0 to 90 minutes. -Referring to Scenario 6-3, what is the probability that the time interval between two consecutive defective light bulbs will be between 10 and 20 minutes?

You were told that the amount of time elapsed between consecutive trades on a foreign stock exchange market followed a normal distribution with a mean of 15 seconds.You were also told that the probability that the time elapsed between two consecutive trades to fall between 16 to 17 seconds was 13%.The probability that the time elapsed between two consecutive trades would fall below 13 seconds was 7%.The middle 60% of the time elapsed will fall between which two numbers?

The probability that a standard normal variable, Z, is between 1.00 and 3.00 is 0.1574.

If we know that the length of time it takes a college student to find a parking spot in the library parking lot follows a normal distribution with a mean of 3.5 minutes and a standard deviation of 1 minute, find the probability that a randomly selected college student will find a parking spot in the library parking lot in less than 3 minutes.

You were told that the amount of time elapsed between consecutive trades on a foreign stock exchange market followed a normal distribution with a mean of 15 seconds.You were also told that the probability that the time elapsed between two consecutive trades to fall between 16 to 17 seconds was 13%.The probability that the time elapsed between two consecutive trades would fall below 13 seconds was 7%.What is the probability that the time elapsed between two consecutive trades will be between 13 and 16 seconds?

SCENARIO 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month, plus a commission.His monthly commission is normally distributed with mean $10,000 and standard deviation $2000.At night he works occasionally as a waiter, for which his monthly income is normally distributed with mean $1,000 and standard deviation $300.John's income levels from these two sources are independent of each other. -Referring to Scenario 6-2, the probability is 0.25 that John's income as a waiter is no more than how much in a given month?

In its standardized form, the normal distribution

SCENARIO 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month, plus a commission.His monthly commission is normally distributed with mean $10,000 and standard deviation $2000.At night he works occasionally as a waiter, for which his monthly income is normally distributed with mean $1,000 and standard deviation $300.John's income levels from these two sources are independent of each other. -Referring to Scenario 6-2, for a given month, what is the probability that John's commission from the jewelry store is at least $12,000?

SCENARIO 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month, plus a commission.His monthly commission is normally distributed with mean $10,000 and standard deviation $2000.At night he works occasionally as a waiter, for which his monthly income is normally distributed with mean $1,000 and standard deviation $300.John's income levels from these two sources are independent of each other. -Referring to Scenario 6-2, for a given month, what is the probability that John's commission from the jewelry store is between $9,000 and $11,000?

The amount of tea leaves in a can from a production line is normally distributed with 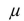= 110 grams and 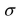= 25 grams.What is the probability that a randomly selected can will contain between 100 and 120 grams of tea leaves?

You were told that the mean score on a statistics exam is 75 with the scores normally distributed.In addition, you know the probability of a score between 55 and 60 is 4.41% and that the probability of a score greater than 90 is 6.68%.What is the probability of a score between 90 and 95?

The interval between patients arriving at an outpatient clinic follows an exponential distribution with mean 15 minutes.What is the probability that a randomly chosen arrival to be less than 15 minutes?

SCENARIO 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month, plus a commission.His monthly commission is normally distributed with mean $10,000 and standard deviation $2000.At night he works occasionally as a waiter, for which his monthly income is normally distributed with mean $1,000 and standard deviation $300.John's income levels from these two sources are independent of each other. -Referring to Scenario 6-2, the probability is 0.95 that John's commission from the jewelry store is at least how much in a given month?

The interval between patients arriving at an outpatient clinic follows an exponential distribution at a rate of 1 patient per hour.What is the probability that a randomly chosen arrival to be more than 2.5 hours?

The amount of time necessary for assembly line workers to complete a product is a normal variable with a mean of 15 minutes and a standard deviation of 2 minutes.So, 60% of the products would be assembled within __________ and __________ minutes (symmetrically distributed about the mean).

Suppose Z has a standard normal distribution with a mean of 0 and standard deviation of 1. The probability that Z is between -2.33 and 2.33 is __________.

The probability that a standard normal variable, Z, is below 1.96 is 0.4750.