Exam 6: Eigenvalues and Eigenvectors
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
Suppose that A is an 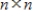 matrix and
matrix and 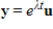 is a solution to the system of linear differential equations
is a solution to the system of linear differential equations 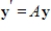 where
where  is an eigenvector of A with associated eigenvalue
is an eigenvector of A with associated eigenvalue 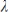 . Let k be any scalar. Then
. Let k be any scalar. Then 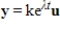 is a solution to the system
is a solution to the system 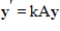 .
.
(True/False)
4.8/5  (32)
(32)
If 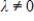 is an eigenvalue of an invertible
is an eigenvalue of an invertible 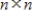 matrix A, then
matrix A, then 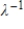 is an eigenvalue of the matrix
is an eigenvalue of the matrix 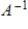 .
.
(True/False)
4.9/5  (31)
(31)
Factor the matrix 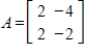 from Question 1 in the form
from Question 1 in the form 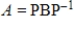 where B is a rotation-dilation matrix.
where B is a rotation-dilation matrix.
(Essay)
4.9/5  (41)
(41)
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 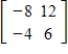 .
.
(Essay)
4.9/5  (35)
(35)
Compute the first two iterations of the Shifted Inverse Power Method, starting with the given 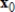 , to determine the eigenvalue of A closest to
, to determine the eigenvalue of A closest to 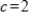 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
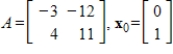
(Essay)
4.9/5  (32)
(32)
If 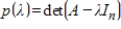 is the characteristic polynomial of an
is the characteristic polynomial of an 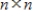 matrix A, and
matrix A, and 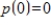 , then A is not invertible.
, then A is not invertible.
(True/False)
4.8/5  (28)
(28)
The coefficient matrix for a system of linear differential equations of the form 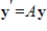 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
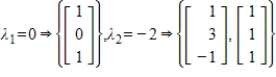
(Essay)
4.9/5  (42)
(42)
The Inverse Power Method applied to the matrix 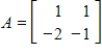 and vector
and vector 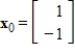 converges.
converges.
(True/False)
4.8/5  (30)
(30)
The coefficient matrix for a system of linear differential equations of the form 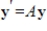 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
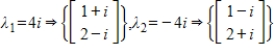
(Essay)
4.8/5  (45)
(45)
Find the matrix A that has the given eigenvalues and corresponding eigenvectors.
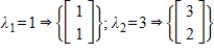
(Essay)
4.7/5  (24)
(24)
Suppose that two countries are in an arms race modeled by the system of differential equations
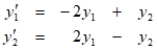 where y1 and y2 are measured in thousands. Find the solution for the system with initial conditions
where y1 and y2 are measured in thousands. Find the solution for the system with initial conditions 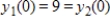 , and use it to predict the long-term amounts of arms held by each country.
, and use it to predict the long-term amounts of arms held by each country.
(Essay)
4.8/5  (31)
(31)
If 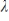 is an eigenvalue of the real
is an eigenvalue of the real 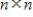 matrix A with corresponding eigenvector
matrix A with corresponding eigenvector  , then
, then 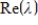 is an eigenvalue of
is an eigenvalue of 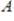 with corresponding eigenvector
with corresponding eigenvector 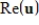 .
.
(True/False)
4.8/5  (36)
(36)
Find the eigenvalues and a basis for each eigenspace for the given matrix.
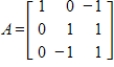
(Essay)
4.9/5  (38)
(38)
Find a basis for the eigenspace associated with eigenvalue 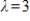 for matrix
for matrix 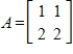 .
.
(Essay)
4.7/5  (38)
(38)
Suppose the 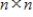 matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
(True/False)
4.9/5  (32)
(32)
Showing 21 - 40 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)