Exam 33: Special Topics in Probability

A child has crayons of eight different colors. The child is to color three squares in a left-to-right row, using a different color for each square. In how many visually different ways can the coloring be done?

These students all want to be on a three-person team: Ann, Bob, Carlita, Diem, Eva, and Franklin. A) In how many different ways could the team be made up? B) What is the probability that Ann, Carlita, and Eva make up the team, if they are chosen at random? C) What is the probability that Ann and Carlita are on the team but Eva is not, if the team is chosen at random?

You have a Bust-a-Balloon stand at a carnival. People pay $3 to throw one dart at balloons. If they miss, you give them a prize worth 10¢. If they burst a balloon, you give them a prize worth $5. Past experience indicates that the probability of a person's missing is 60%. A) Find the expected value of this carnival game from your point of view. B) What does your answer in part A mean? (Give a fake answer for A if you did not figure A out.)

A fellow student asks, "If you are choosing three letters from the alphabet, is ABD a permutation or a combination? And how do you tell?"

You pay $1 each time you play the following game. Flip two fair coins. If they both land heads up, you win 50¢. If they land mixed, one head up and one tail up, you get 75¢. If they both land tails up, you get $3. A) Find the expected value of the game. B) What does your result in part A mean if you play the game many, many times?

A) What is the probability of exactly four heads on the toss of eight honest coins? Show your work, but you do not have to carry out extensive calculations. B) What is the probability of exactly two tails on the toss of eight honest coins? Show your work, but you do not have to carry out extensive calculations. C) What would have to be changed in parts A and B if the coins were not honest, say P(H) = 0.6? Be specific; do not say just, "The probabilities would change."

Once a certain disease is discovered in a patient, the probability of its being successfully treated is 50-50. Suppose the disease is discovered in four people. What is the probability that at least three of them are successfully treated?

There are four balls in a bag: one red, two blue, and one green. If you draw out a red ball, you win $20. If you draw out a blue ball, you win $2. If you draw out a green ball, you win $10. Should you pay $9 to play this game? Why or why not? (Argue in terms of expected value.)

Experiment: Spin the spinner below then select one ball from the box designated by the spinner. 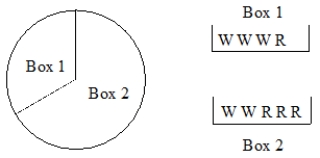A) In the experiment, selecting R pays $2 and selecting W pays $4. It costs $3 to play. What is the expected value? B) What does your answer in part A mean?

Spin-and-Win is under new management. The new management has changed the spinner as below and now charges $1 per spin. (The person spinning wins the amount pointed to by the spinner.) 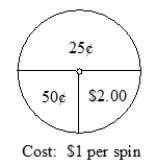A) What is the expected value for this game? (Show your work.) B) What does your answer in part A mean if there are 1000 customers who play the game in a week?

In a certain game, on each turn you make moves by spinning the spinner below, according to these rules: 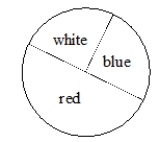Red: move one space Blue: move three spaces White: lose your turn (move zero spaces) If you play the game a long time, how many spaces would you move each time, on average?

The expected value for one Super Lotto game is ^-41¢. What does that mean?

A) You are buying a holiday gift for each of five young nieces/nephews. You have found eight different books at one store that would be good choices for any of the children. In how many ways can you buy five of the eight books? B) Now you are ready to wrap the books. You have six different kinds of paper and four kinds of ribbon. You decide to use a different paper-ribbon combination for each book. In how many ways could one of the presents be wrapped? C) You also buy a chocolate star, a chocolate snowman, a chocolate candle, a peppermint cane, and a jelly-bean tree. You decide to give one candy each to the five children. Knowing that only one of the five children does not like chocolate, in how many ways can you assign the candies to the five children?

Spin-and-Win is under new management. The new management has changed the spinner, as below, and now charges $1 per spin. (The person spinning wins the amount pointed to by the spinner.) 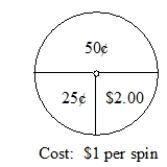A) What is the expected value for this game? (Show your work.) B) What does your answer in part A mean if there are 1000 customers who play the game in a week?

In 30 tosses of a dishonest coin with probability of heads = 0.7, what is the probability of getting the following? (Show your work, but you do not have to carry out extensive calculations.) A) Exactly two heads B) Two or more heads

A) What is the difference between a permutation and a combination? B) A baseball team has nine players. How many possible batting orders are there, assuming that the manager just makes one up at random? C) If you are on the team, how many batting orders will be possible if you are the first batter?